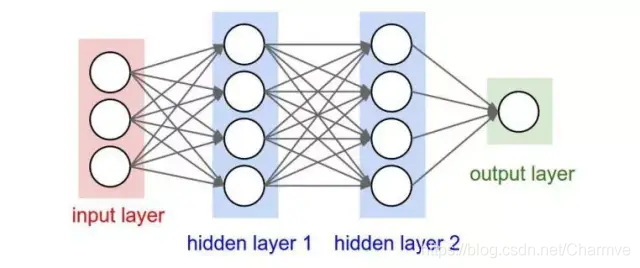
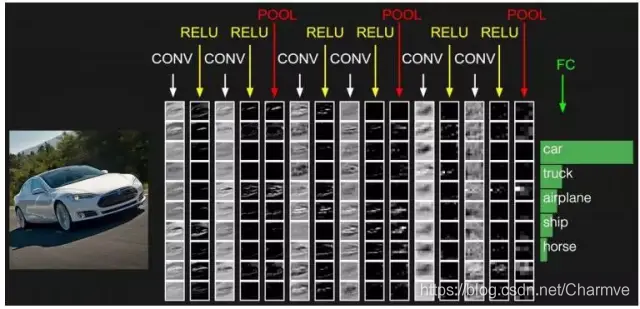
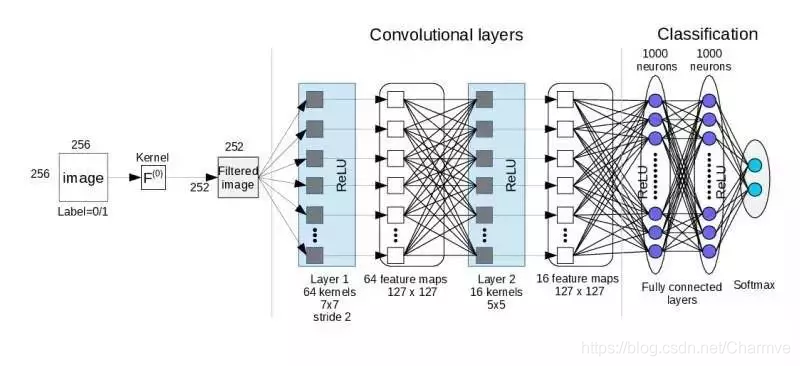
卷积层的参数计算:
- 卷积后feature map边长: outputSize =(originalSize + paddingX2 – kernelSize)/ stride + 1 (其中outputSize是卷积之后得到的feature map的边长,originalSize是输⼊图的边长,padding是填充的⼤⼩,kernelSize是卷积核的边长,stride是步长)
- 卷积层的可训练的参数个数: trainNum = (outputSize X outputSize + 1) X kernelNum (其中kernelNum是卷积核的个数,加1是因为每⼀个卷积核有⼀个bias参数)
- 卷积层的连接数: connectNum = (kernelSize X kernelSize) X (outputSize X outputSize) X kernelNum
- 卷积层的神经元个数: neuralNum = (outputSzie X outputSize) X kernelNum
采样层的参数计算:
- 采样后map的边长: outputSize =(originalSize + paddingX2 – kernelSize)/ stride + 1 (其中outputSize是卷积之后得到的feature map的边长,originalSize是输⼊图的边长,padding是填充的⼤⼩,kernelSize是卷积核的边长,stride是步长)
- 采样层可训练的参数个数: trainNum = (1+ 1) X kernelNum (其中kernelNum是卷积核的个数)
- 采样层的连接数: connectNum = (kernelSize X kernelSize) X (outputSize X outputSize) X kernelNum
- 采样层的神经元个数: neuralNum = (outputSzie X outputSize) X kernelNum