刚学习深度学习的时候，在网上曾经看过很多资料，始终搞不懂，为什么大家都说神经网络为什么能够无限逼近任意连续函数。大家普遍认为，理论上只要神经元足够多，神经网络足够大，就可以实现

后来知乎有个人写了偏文章解释了一下，有兴趣的可以移步这里：https://zhuanlan.zhihu.com/p/25590725

我困惑的根源在于：

1. 神经网络说白了就是一个矩阵，神经元之间的链接就是各种矩阵运算
2. 有很多激活函数是“线性”的，比如ReLU及其各种变种

当然，有些人认为ReLU是非线性激活函数，其实也没有错。但是我个人理解，叫分段线性函数，更合适一些。

那么问题来了，如果一个神经网络中，全部使用线性单元，无论经过多少次矩阵运算，最终训练出来的网络，不还是一个线性函数吗？

比如，如果我只用ReLU激活函数，来训练一个 y = sin(x) 会怎么样？

如下，构造一个5层，每层有20个激活单元，只使用ReLU激活函数的神经网络。训练 10000 次

x_tensor = torch.linspace(-20, 20, 40)
x_data = torch.unsqueeze(x_tensor, 1)
y_data = torch.sin(x_data)

myNet = nn.Sequential(
        nn.Linear(1, 20),
        nn.ReLU(),
        nn.Linear(20, 20),
        nn.ReLU(),
        nn.Linear(20, 20),
        nn.ReLU(),
        nn.Linear(20, 20),
        nn.ReLU(),
        nn.Linear(20, 20),
        nn.ReLU(),
        nn.Linear(20, 1)
        )


optimzer = torch.optim.SGD(myNet.parameters(), lr=0.01)
loss_func = nn.MSELoss()

最后得到的函数是这样的：其中黄色的是我用来训练的数据，蓝色的是最终训练出来的函数

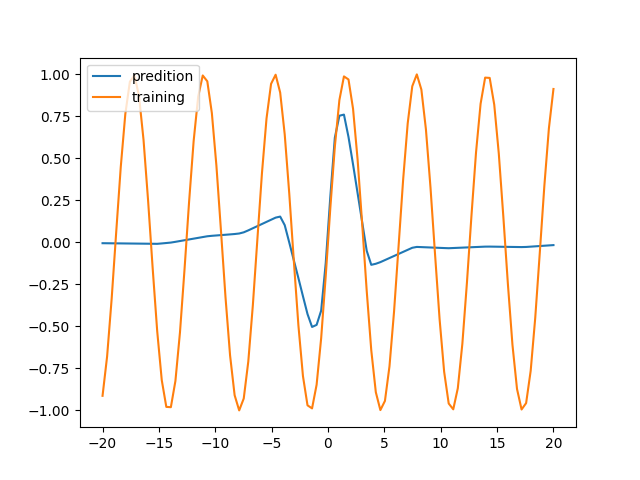
看起来辨识度不够，只有-5～5区间吻合程度比较高，超过这个区间方差非常大

训练 50000 此，再看一下

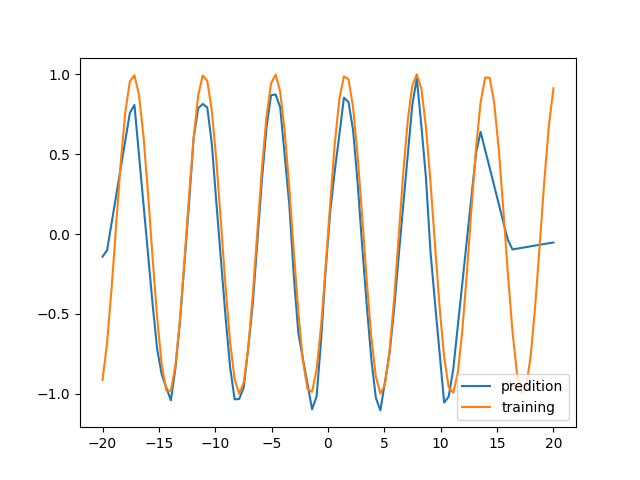
现在看起来比较吻合了。但是实际果真如此吗？这个神经网络能够实现任意输入的 sin(x) 求解？注意前面我们在训练的时候，训练神经网络使用的都是 -20 ~ 20 范围的数据集，并且都是整数。

如果要评估这个神经网络的能力，还得看这个范围之外的数据的表现能力如何。为此，我们构造两种类型的新数据，来评估这个网络的泛法能力：

1. 构造 -20 ~ 20 之外的数据
2. 构造 -20 ~ 20 之内的小数（之前训练用的都是整数）

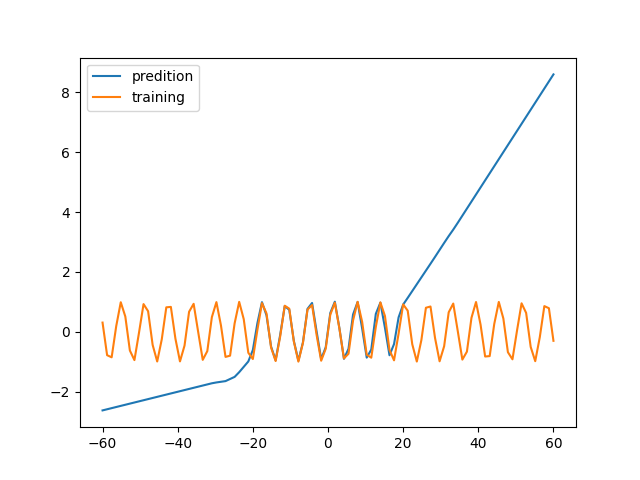
1）看 -60 ~ 60 范围内的数据

2）还是看 -20 ~ 20 范围内的数据，但是粒度更细

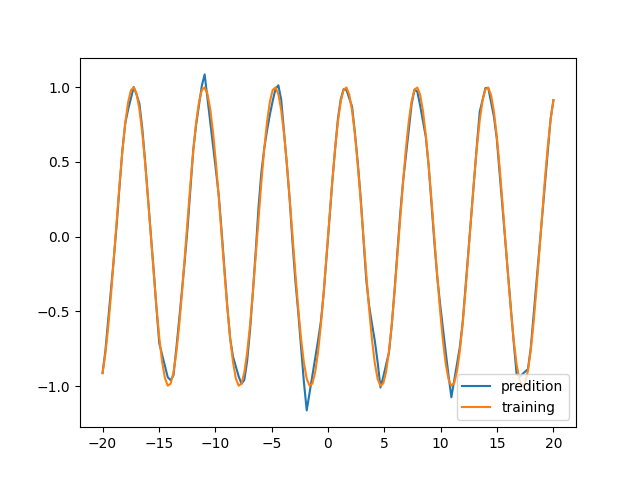
同样是都没见过的数据，为什么第二种场景拟合的很好，第一种就方差非常大呢？这也是一个很神奇的地方。不过，总的来说，这个网络的泛化能力还是很差

从目前的测试来看：训练集内的数据，看起来是可以进行非线性拟合的。但是训练集外的数据，方差太大，几乎没有拟合。所以，我们还不能说我们把 sin(x) 函数训练出来了。后面再研究一下