第一次看 ng 斯坦福机器学习这门课程的时候，就没看懂交叉验证是怎么回事。
参考视频: 10 – 3 – Model Selection and Train_Validation_Test Sets (12 min).mkv
ng 在讲交叉验证的时候，是这么举例的
假设我们要在10个不同次数的二项式模型之间进行选择：
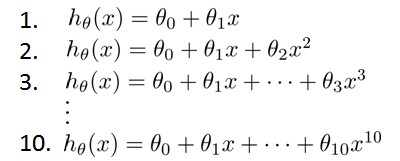
显然越高次数的多项式模型越能够适应我们的训练数据集，但是适应训练数据集并不代表着能推广至一般情况，我们应该选择一个更能适应一般情况的模型。我们需要使用交叉验证集来帮助选择模型。 即：使用60%的数据作为训练集，使用 20%的数据作为交叉验证集，使用20%的数据作为测试集
原文链接：https://zhuanlan.zhihu.com/p/29360425
正则化（Regularization）是机器学习中一种常用的技术，其主要目的是控制模型复杂度，减小过拟合。最基本的正则化方法是在原目标（代价）函数 中添加惩罚项，对复杂度高的模型进行“惩罚”。其数学表达形式为：
式中 、
为训练样本和相应标签，
为权重系数向量；
为目标函数，
即为惩罚项，可理解为模型“规模”的某种度量；参数
控制控制正则化强弱。不同的
函数对权重
的最优解有不同的偏好，因而会产生不同的正则化效果。最常用的
函数有两种，即
范数和
范数，相应称之为
正则化和
正则化。此时有：
本文将从不同角度详细说明 、
正则化的推导、求解过程，并对
范数产生稀疏性效果的本质予以解释。
nn.Linear 定义：https://pytorch.org/docs/stable/generated/torch.nn.Linear.html#torch.nn.Linear
class torch.nn.Linear(in_features: int, out_features: int, bias: bool = True)
其中：
False, the layer will not learn an additive bias. Default: Truepytorch 本身是没有神经网络层的概念的，所以如果我们要定义一个神经网络，需要通过 torch.nn.Module 来实现
假设我们有很多样本数据，符合模型 y = wx + c，我们也可以用 torch 来直接生成一些随即样本数据
x = torch.unsqueeze(torch.linspace(0, 1, 300),dim=1)
y = 2 * x + torch.rand(x.size())之前我在讲理解最大似然估计 http://0fd.org/2017/06/10/understand-the-maximum-likelihood-estimation/ 的时候，讲了两个例子，不过都很简单，今天来讲讲怎么用最大似然估计来求解线性回归方程，不管是一元还是多元
线性回归方程如下：
y = \theta_1 x_1 + ... + \theta_n x_n = \sum_{i=1}^{n} \theta_i x_i现在假设我们有 m 组样本数据，(y^1, x_{(1 \sim n)}^1), (y^2, x_{(1 \sim n)}^2), ..., (y^m, x_{(1 \sim n)}^m)，我们怎么用最大似然估计来求解\theta呢？
神说，要有正态分布，就有了正态分布。
神看正态分布是好的，就让随机误差服从了正态分布。
— 创世纪—数理统计
转载自：https://cosx.org/2013/01/story-of-normal-distribution-1
学过基础统计学的同学大都对正态分布非常熟悉。这个钟形的分布曲线不但形状优雅，它对应的密度函数写成数学表达式
\displaystyle f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{{(x-\mu})^2}{2\sigma^2}}
也非常具有数学的美感。其标准化后的概率密度函数
\displaystyle f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}
更加的简洁漂亮，两个最重要的数学常量 (\pi)、(e) 都出现在这公式之中。在我个人的审美之中，它也属于 top-N 的最美丽的数学公式之一，如果有人问我数理统计领域哪个公式最能让人感觉到上帝的存在，那我一定投正态分布的票。因为这个分布戴着神秘的面纱，在自然界中无处不在，让你在纷繁芜杂的数据背后看到隐隐的秩序。
