nn.Linear 定义:https://pytorch.org/docs/stable/generated/torch.nn.Linear.html#torch.nn.Linear
class torch.nn.Linear(in_features: int, out_features: int, bias: bool = True)
其中:
- in_features – 每次输入的样本数,默认是1
- out_features – 每次输出的样本数,默认也是1
- bias – If set to
False, the layer will not learn an additive bias. Default:True
pytorch 本身是没有神经网络层的概念的,所以如果我们要定义一个神经网络,需要通过 torch.nn.Module 来实现
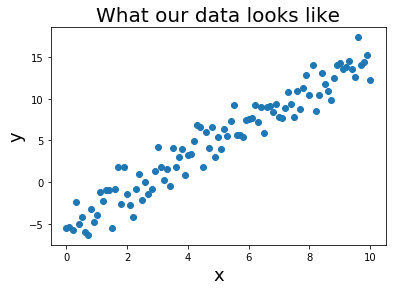
假设我们有很多样本数据,符合模型 y = wx + c,我们也可以用 torch 来直接生成一些随即样本数据
x = torch.unsqueeze(torch.linspace(0, 1, 300),dim=1)
y = 2 * x + torch.rand(x.size())