在我们实际测试的过程中，我们发现分离式架构受模型和负载的影响其实是非常大的。

不同的模型，不同的负载，收益大小很不一样

1. 模型：模型大小，开不开 gqa，等
2. 负载：输入长度、输出长度、请求的 qps，等

那我们怎么知道什么场景下适合用分离式架构呢？

这篇文章我们从 decode 阶段的理论计算上来尝试推导一下，看模型和负载是如何影响分离式架构的收益的

1. Decode 计算和访存需求

参考：FASTDECODE: High-Throughput GPU-Efficient LLM Serving using Heterogeneous

decode 时间理论计算（假设默认开启 GQA = 8，量化 int8，xx）：

	batch 计算	batch 访存量
S-part	24bh²	(12h² + 10bh) * sizeof(int8) = 12h² + 10bh
R-part	4bhs	2bhs * sizeof(int8) = 2bhs

注意：

1. 12h² + 10bh，不管是大模型还是小模型，10bh耗时占比1/1000，所以10bh可以直接忽略
2. R-part的计算耗时 4bhs/312，也是要远远小于其他3项，基本可忽略

所以整个 decode 阶段的耗时，可以按如下计算

TBT = \frac{24blh^2}{312} + \frac{12lh^2}{2} + \frac{2blhs}{2 * GQA} = b(\frac{24lh^2}{312} + \frac{2lhs}{2 * GQA}) + \frac{12lh^2}{2}

因此：TBT 是一个bs的线性函数

2. 分离式架构的理论收益公式

2.1 干扰程度

分离收益的前提，取决于干扰的程度，干扰越大，分离后的收益越大假设一个模型：

1. tbt：单token输出时间
2. ttft：首token计算时间
3. s：输入长度
4. n：输出长度
5. λ：请求进来的速率

单个请求端到端的时间：e2e = tbt * n + ttft

受干扰的时间比例： β= \frac{e2e * λ * ttft}{e2e} = λ * ttft

2.2. BS和TBT相关性函数

从第一节我们知道，TBT是一个BS的线性函数

TBT = \frac{24blh^2}{312} + \frac{12lh^2}{2} + \frac{2blhs}{2 * GQA} = b(\frac{24lh^2}{312} + \frac{2lhs}{2 * GQA}) + \frac{12lh^2}{2}

这个函数有一个拐点：当 bs 大约 60 （70b模型）的时候，b(\frac{24lh^2}{312} + \frac{2lhs}{2 * GQA}) = \frac{12lh^2}{2}，简化一下 b(\frac{h}{13} + \frac{s}{8}) = 6h

这个拐点越大，说明TBT对bs约不敏感

所以上面公式可以简化如下：f(BS) = t_1 + \frac{t_1}{BS_g} * BS

其中：

1. t1 表示 bs = 1 时的 TBT，主要就是 \frac{12lh^2}{2}
2. \frac{t1}{BS_g}表示bs每增加1，对应增加的 decode 时间，$BS_g$是一个BS 性能拐点，不同模型不一样

假设耗时允许增加 β，从BS提升到BS_{2}

t_1 + \frac{t_1}{BS_g} * BS_2 = (1+β) * (t_1 + \frac{t_1}{BS_g} * BS)

解这个方程，得：

BS_2 = BS + β * (BS+BS_g)

2.3. 理论收益计算

首先要明确一个基本认知：有收益的前提一定取决于干扰的程度，因为如果没有干扰，分离和不分离性能就是一样的，分离之后能提batch size，分离前也一定可以提batch size。（而且分离后，decode和prefill机器都更密集了，也就是计算的并行度变低，甚至可能有负向收益）

由于分离式架构，核心是提高 decode 性能

我们假设一个推理服务，需要 P 个 prefill 机器，需要 D 个 decode 机器

那么分离式架构带来的收益是：

D_{节省比例} = D_{机器占比} * BS_{提升空间} = \frac{D}{D+P} * BS_{提升空间}

那么，这个BS_{提升空间}怎么计算呢？

分离后BS会放大2次，一次是纯分离架构变化引入的，一次是节省D机器带来的，只有后者是我们的收益空间

1）分离后的BS_1

这种情况下，BS也是会变大的，因为机器数从 D+P 变成了 D

BS * (1-β) * (D+P) = BS_{1} * D BS_{1} = BS * (1-β) * \frac{D+P}{D}

2）保证TBT不退化情况下，BS的理论上限BS_2

从第一节我们知道，中断带来的时间占比是 β = λ * ttft，由于分离后，干扰消失，所以在 TBT 不退化的情况下，BS可以提升（允许增加 β时间 ）

BS_2 = BS + β * (BS+BS_g)

因此

BS_{提升空间} = \frac{BS_2 - BS_1}{BS_2} = 1 - \frac{BS_1}{BS_2} = 1 - \frac{(1-β)\frac{D+P}{D}}{1+β(1+BS_g / BS)}

。

D_{节省比例} = \frac{D}{D+P} * BS_{提升空间} = \frac{D}{D+P} - \frac{1-β}{1+β(1+72/BS)} = (1-λ*TTFT) - \frac{1-β}{1+β(1+BS_g/BS)}

。

D_{节省比例} = (1-β) - \frac{1-β}{1+β(1+BS_g/BS)}

https://hs.luomashu.com/

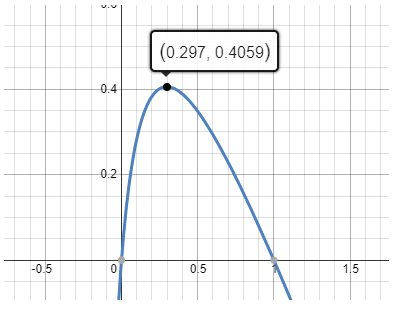
这个公式受3个核心因素的影响：

1. β：干扰的比例，干扰越小，提升空间就比较有限，干扰越大也不行，这样D机器就会很少，最终能节省下来的机器就越少
2. BS：当前SLO约束下的最大BS，和β有一定相关性
3. BS_g是模型的 BS 拐点

3. 模型大小对BS拐点的影响

我们假设 s = 1.5k

3.1. 对7b模型：h = 4k

7b 模型都不开 GQA，默认是 1

b(\frac{24lh^2}{312} + \frac{2lhs}{2 * GQA}) = \frac{12lh^2}{2}

所以有：

b(\frac{24lh^2}{312} + \frac{2lhs}{2 * 1}) = \frac{12lh^2}{2}，简化一下b(\frac{h}{13} + \frac{s}{2}) = 6h

b 的拐点是大约是 23

3.2. 对70b模型：h = 8k，GQA = 8

这个上面计算过了，60

3.3. 对175b模型：h = 12k，GQA = 8

175b 模型都开 GQA = 8

b(\frac{24lh^2}{312} + \frac{2lhs}{2 * GQA}) = \frac{12lh^2}{2}

所以有：

b(\frac{24lh^2}{312} + \frac{2lhs}{2 * 8}) = \frac{12lh^2}{2}，简化一下b(\frac{h}{13} + \frac{s}{8}) = 6h

b 的拐点是 64

4. 输入输出对干扰的影响

和模型不同的是，输入输出，其实影响的是干扰程度的大小

从第一节我们知道，受干扰的时间比例： β = \frac{e2e * λ * ttft}{e2e} = λ * ttft

这是一个单调函数（实际情况可能不是线性的，应该是非线性的）， λ * ttft 越大，干扰越大

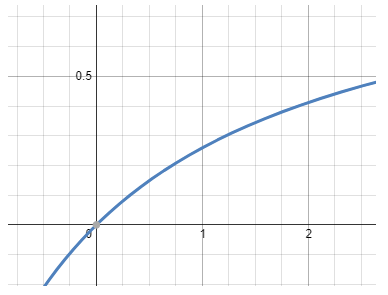
假设：

1. 一个模型在线上长期运行，但是他的负载（输入输出长度）是会发生变化的
2. 但是系统承诺的 SLO 不会变化。对推理服务的 decode 阶段来说，SLO 和 batch size 单调正相关，SLO=f(b)

根据经典的排队理论：

服务的平均排队长度BS = 请求进来的速率 λ * 平均服务时间E2E(n * TBT)，同时BS又是一个 f(SLO)的公式

因此：

f(SLO) = λ * (n * TBT) λ = \frac{f(SLO)} {(n * TBT)}

代入上面的干扰程度公式：

β = λ * ttft = \frac{f(SLO)} {(n * TBT)} * ttft

我们知道，这是一个单调函数， λ * ttft 越大，干扰越大f(SLO) 是定量，TBT也是个相对定量（拐点之前，TBT退化很小），那这个公式里唯一的2个变量就是，输出长度 n 和 ttft

故，得结论：输入越长（ttft越大）、输出越短（n越小），干扰越大，分离式带来的收益越明显。

5. 综合结论

收益公式：

D_{节省比例} = (1-β) - \frac{1-β}{1+β(1+\frac{BS_g}{BS})} β = λ * ttft = \frac{f(SLO)} {(n * TBT)} * ttft

3个核心因子：

1. β干扰时间比例。可以根据线上实际的请求速率λ和TTFT估算
2. BS_g：BS的性能拐点（BS从1涨到多少，TBT会翻倍），大概在 46~64 之间，主要受模型大小影响，token长度也会有一定影响
3. BS：当前 SLO 约束下的极限 BS

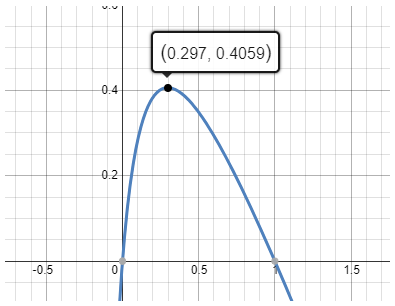
由收益公式，可得出如下关键结论：

1. 模型越大，bs拐点越大。在拐点之前，bs提升对decode性能影响越小（小模型拐点是bs=16，大模型int8量化拐点是46~64）
2. 输入输出长度：决定了干扰程度，输入越长，输出越短，干扰越大，分离后的收益越明显

6. 175b 模型收益评估

假设一个 175B模型，按照 GQA = 8，int8量化，估算，BS_g就是 60

D_{节省比例} = (1-β) - \frac{1-β}{1+β(1+\frac{60}{BS})}

1. β：假设请求速率大概是每秒 1.5 个请求，TTFT = 350ms，所以 β = 1.5 * 0.35 = 0.525
2. BS：假设满足 SLO 情况下的极限BS 是 20

所以函数：

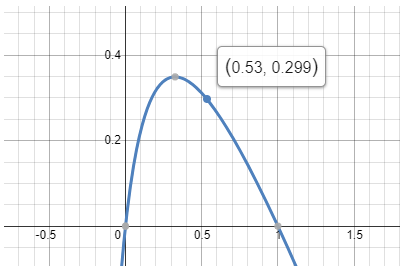
D_{节省比例} = 0.3 对应吞吐提升：\frac{1}{1-0.3} = 42\%

对大部分模型来说，分离式架构的吞吐提升大概在 20% ~ 40% 左右