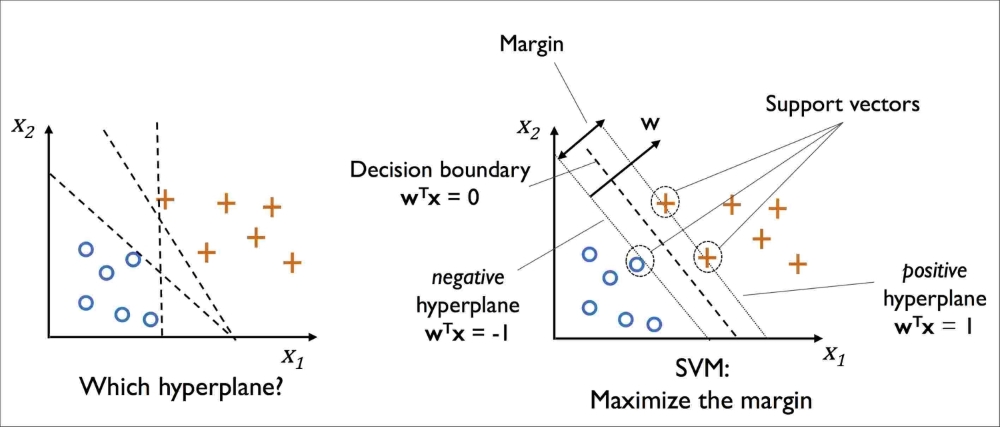
学SVM的时候你会经常听到拉格朗日对偶。拉格朗日对偶是凸优化问题中比较常见的一个手段,关于凸优化,强烈建议Boyd的《凸优化》这本书,总结的很好
lagrange 对偶的基本思想,是将原目标函数,通过对其约束条件的加权求和,变成一个广义的目标函数。从而将一个M个变量N个约束的目标函数转换成一个M+N个变量的目标函数,再得到这个函数的对偶函数
这个对偶函数非常有用,因为他有几个重要性质:
- 无论原始问题是不是凸的,对偶问题一定是凸的,可以证明
- 对偶问题给出了原始问题的一个下界,可以证明
- 当满足一定条件时,对偶问题的解和原问题的解是等价的,可以证明