https://mp.weixin.qq.com/s/uK1owRF53FW4WI7nldYadg
https://arxiv.org/pdf/2311.15566.pdf
业界首个,在可抢占式实例上运行的分布式大语言模型(LLM)服务系统
目标:LLM 降本 -> 抢占式 GPU 实例 -> 怎么更好的用这些抢占实例
相比直接使用抢占式GPU实例,SpotServe 可以将推理引擎的长尾延迟降低 2.4x – 9.1x
LLM 特点:
- 高计算量
- 大内存占用
无论是哪一点,都意味着成本昂贵
把 LLM 运行在随时可抢占的 GPU 实例上
传统的方法,MArk、Cocktail,单实例多GPU卡,运行一个 small DNN 模型,通过请求重定向或者冗余计算来处理抢占,但是这种方式只是和数据并行这种小的DNN模型,不适合LLM
LLM 会同时使用数据并行、模型并行、流水线并行多种技术,单个实例抢占会影响整个多个实例的计算结果
所以需要有更有效的方法
亮点:第一个做推理容错的论文(其他的都是在做训练的容错)
SpotServe 的创新点:
- 动态配置并行度
- 实例迁移优化(复用模型参数、中间结果,减少迁移后的传输数据量):aws 抢占GPU实例,迁移后冷启动需要2m
- 高效利用宽限期(30s,尽量不中断推理)
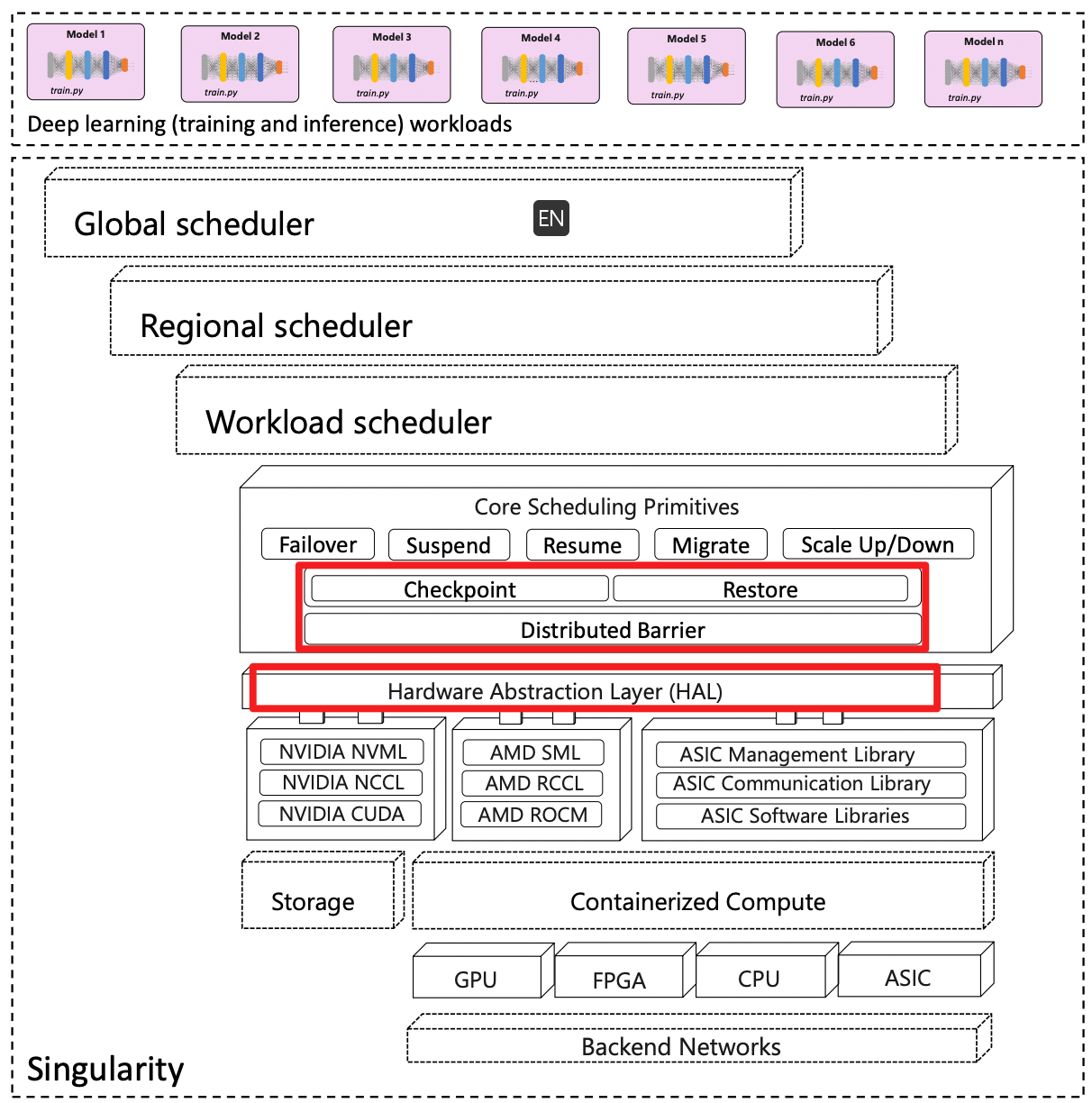
1. 背景
1.1. Generative LLM Inference
当前类似的系统:
- FasterTransformer
- Orca
- FairSeq
- Megatron-LM
单次推理的总耗时,分析
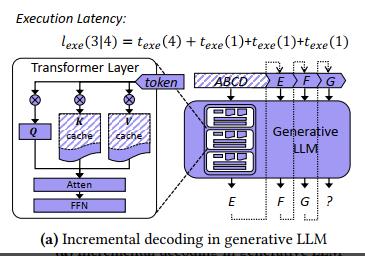
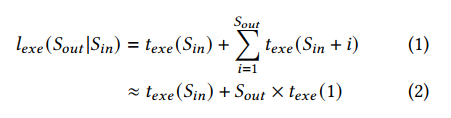
texe(Sin) 是输入序列的解码时间
Sout 是生成的 token 数量,texe(1) 是生成每个 token 的时间
KV cache 技术可以将每个 token 的生成时间优化到接近常量 (i.e., 𝑡𝑒𝑥𝑒 (1) in E.q.(2) and Figure 1a).