1. Measuring the Mismatch: The vllm-kl Metric
\small{\mathbb{E}_{s\sim d_{\textcolor{red}{\pi^\text{vllm}_\theta}}}\left[\text{KL}\left(\textcolor{red}{\pi^\text{vllm}_\theta}\left(\cdot|s\right),\textcolor{blue}{\pi^\text{fsdp}_\theta}\left(\cdot|s\right)\right)\right] = \mathbb{E}_{s\sim d_{\textcolor{red}{\pi^\text{vllm}_\theta}},a\sim {\textcolor{red}{\pi^\text{vllm}_\theta}\left(\cdot|s\right)}} \left[\log\left(\frac{\textcolor{red}{\pi^\text{vllm}_\theta}(a|s)}{\textcolor{blue}{\pi^\text{fsdp}_\theta}(a|s)}\right)\right],}但是代码用的是 kl3 散度
kl = \frac{\pi_1}{\pi_2} - log(\frac{\pi_1}{\pi_2}) - 1rollout_log_probs = batch.batch["rollout_log_probs"] # pi_vllm actor_old_log_probs = batch.batch["old_log_probs"] # pi_fsdp response_mask = batch.batch["response_mask"] log_ratio = actor_old_log_probs - rollout_log_probs vllm_k3_kl_matrix = torch.exp(log_ratio) - log_ratio - 1 vllm_k3_kl = masked_mean(vllm_k3_kl_matrix,response_mask)
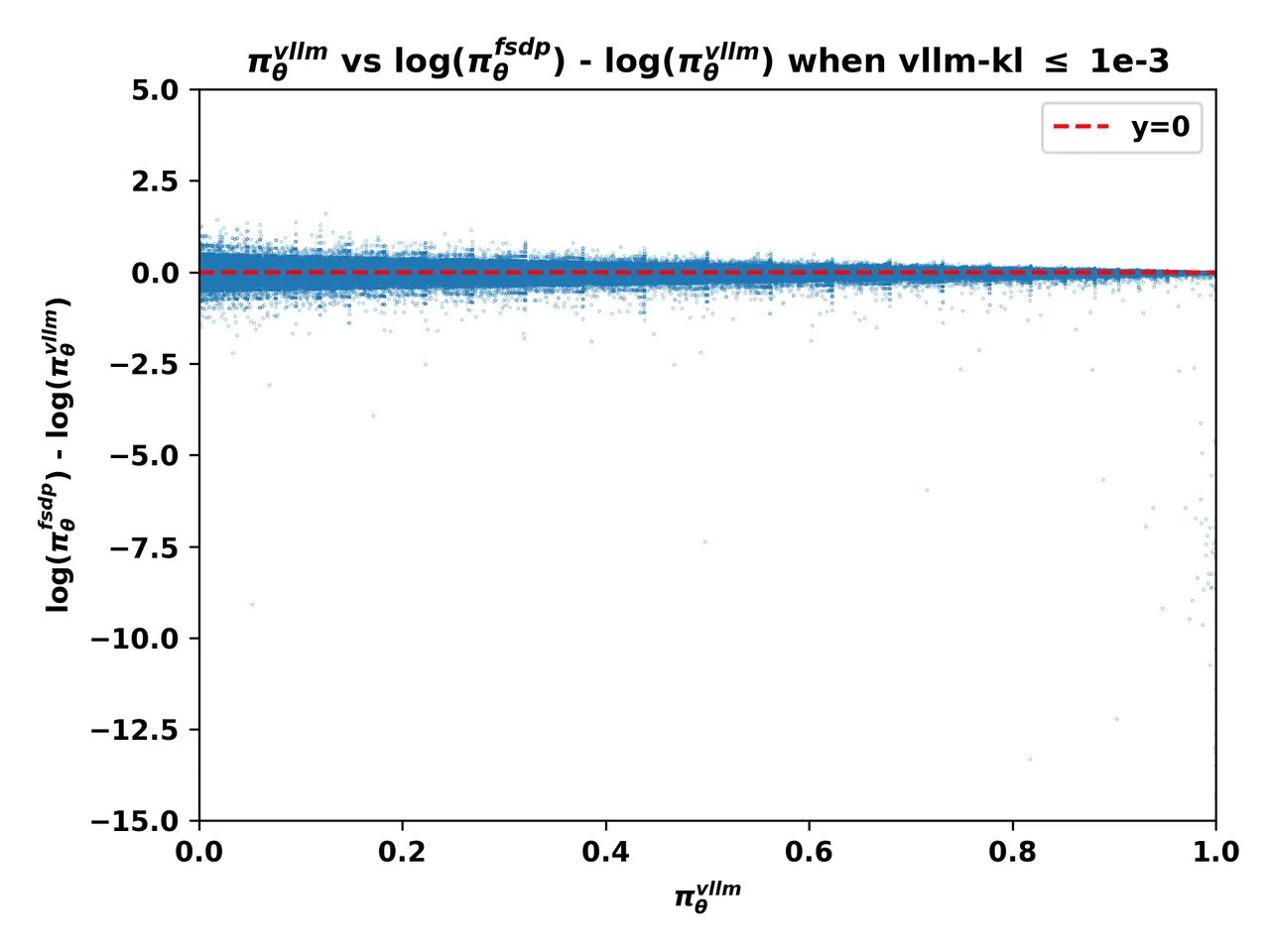
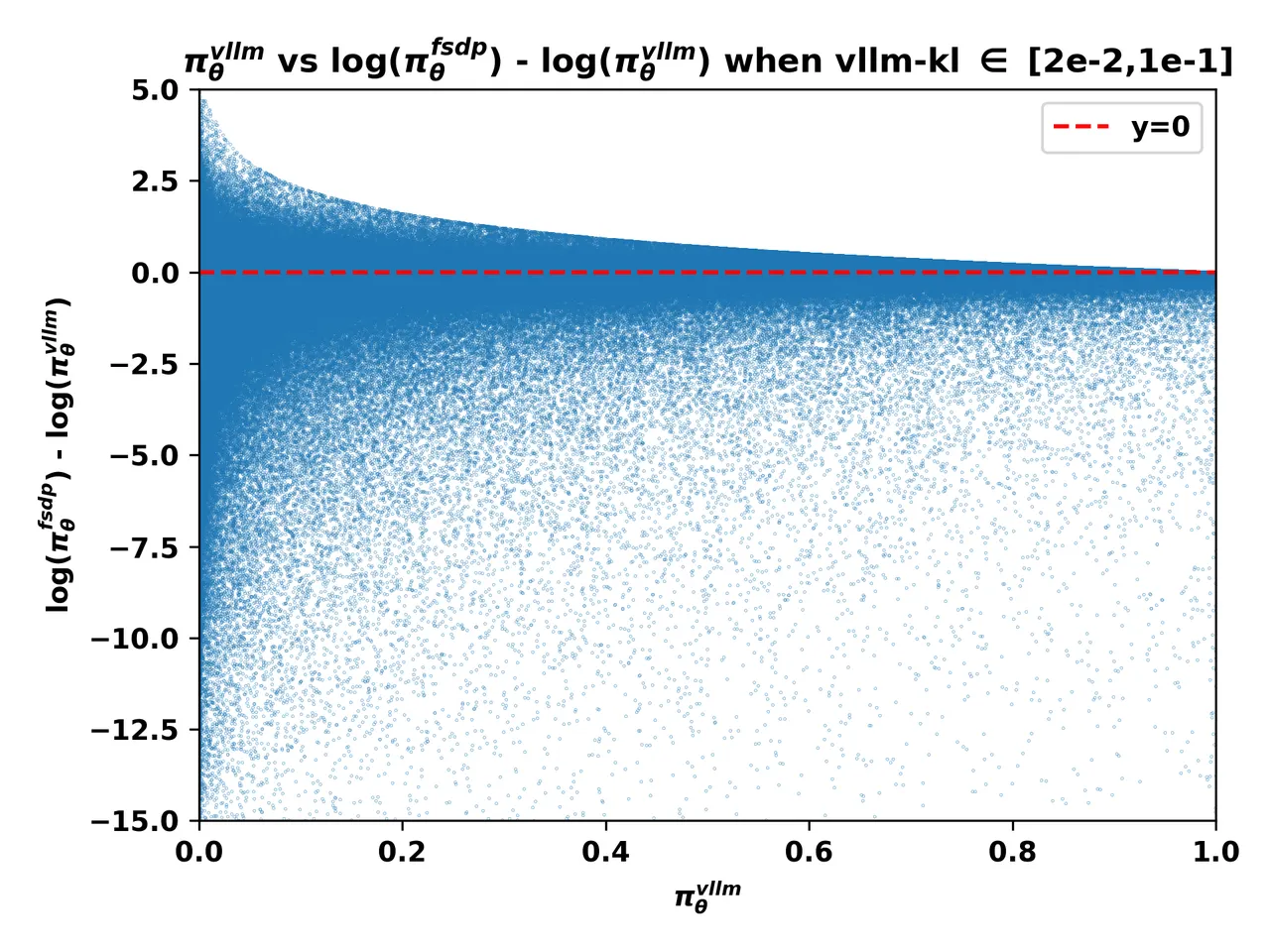
2. The Smoking Gun: The Low-Probability Token Pitfall
这个洞察意义其实不大,这个相关性不需要通过数学分析来找到这种洞察,vllm-kl很小,从数学上就能直接推导出 \frac{\pi_{fsdp}}{\pi_{vllm}} 会很发散
不过这里有一个重要的洞察是:当熵很大的时候,fsdp的log_probs要比vllm的log_probs小