线性回归产生的预测值y=\theta^T x是实值，而逻辑回归通常是要解决分类问题。用线性回归来解决分类问题效果是很差的

分类问题在生活中是很常见的，二项逻辑回归模型有如下的条件概率分布

1. 成功概率：P(Y=1|X) = \frac {1}{1+e^{-\theta^T x}}
2. 失败概率：P(Y=0|X) = 1- \frac {1}{1+e^{-\theta^T x}}

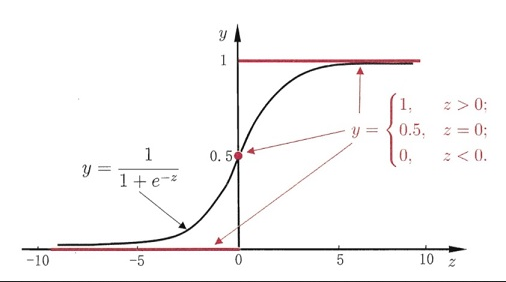
假定h_\theta = \frac {1}{1+e^{-\theta^T x}}，我们可以构造最大似然概率：

L(\theta) = \prod_{i=1}^{m} P(y_i|x_i;\theta) = \prod_{i=1}^{m} (h_{\theta}(x))^y(1-h_{\theta}(x))^{(1-y)}

对上面公式两边去对数，最终转化为求最小值问题

L(\theta) = -\frac {1}{m} \sum_{i=1}^{m} [y_ilogh_{\theta}(x_i) + (1-y_i)log(1-h_{\theta}(x_i))]

求极值人手工算是很简单的，关键是怎么让计算机来算？计算机可不懂推导的

答案是：梯度下降算法

梯度下降法求解的公式是：\theta_{j+1} = \theta_j - \alpha \frac {\delta L(\theta)}{\delta \theta}

将对数似然函数代入梯度下降公式，得到：

\theta_{j+1} = \theta_j - \alpha \frac {1}{m} \sum_{i=1}^{m} x_i|[h_{\theta} (x_i) - y_i]

其中\alpha是步长，可以在实际应用中大概指定一个

最终随着迭代次数不断变多，\theta_j 会越来越收敛到真实值附近