学SVM的时候你会经常听到拉格朗日对偶。拉格朗日对偶是凸优化问题中比较常见的一个手段,关于凸优化,强烈建议Boyd的《凸优化》这本书,总结的很好
lagrange 对偶的基本思想,是将原目标函数,通过对其约束条件的加权求和,变成一个广义的目标函数。从而将一个M个变量N个约束的目标函数转换成一个M+N个变量的目标函数,再得到这个函数的对偶函数
这个对偶函数非常有用,因为他有几个重要性质:
- 无论原始问题是不是凸的,对偶问题一定是凸的,可以证明
- 对偶问题给出了原始问题的一个下界,可以证明
- 当满足一定条件时,对偶问题的解和原问题的解是等价的,可以证明
1)对偶的形式化定义
考虑一个标准的最优化问题:
\begin{aligned} \min \qquad & f_0 (x) \\ s.t. \qquad & f_i (x) \le 0, i = 1, ..., m \\ & h_i (x) = 0, i = 1,..., p \end{aligned}它的广义拉格朗日函数是:
L(x,\lambda,v) = f_0 (x) + \sum\limits_{i=1}^{m} \lambda_i f_i (x) + \sum\limits_{i=1}^p v_i h_i (x)它的拉格朗日对偶函数是:
g(\lambda,v) = \min\limits_{x} L(x,\lambda,v) = \min\limits_x \left ( f_0 (x) + \sum\limits_{i=1}^{m} \lambda_i f_i (x) + \sum\limits_{i=1}^p v_i h_i (x) \right )简单来说,就是说对于任意的一组(α,β),都要找到一个x使得L最小,不同的(α,β)对应不同的g函数值。这个理解起来有点费脑筋,但是想清楚非常重要
2)示例:最小二乘
假设我们要优化一个最小二乘问题,比如
\begin{aligned} \min \ & x^{T} x \\ s.t. \qquad & Ax=b \end{aligned}这个问题没有不等式约束,有 p 个(线性)等式约束,其 lagrange 函数L(x,v) = x^T x + v^T (Ax-b),对偶函数是g(v) = \min\limits_x L(x,v)
因为L是关于x的二次凸函数,所以可以通过求极值,得到L函数的最小值,如下
\bigtriangledown_x L(x,v) = 2x + A^T v = 0可见,L函数在点 x = -1/2 A^T v 处,总能得到最小值,因此对偶函数为
g(v) = L(-(1/2)A^T v, v) = -(1/4)v^T AA^T v - b^T v这个函数就是原目标函数的一个下界
-(1/4)v^T AA^T v - b^T v \le \min\limits_x{(x^T x | Ax = b)}。
3)证明:对偶问题是原始问题的下界
假设p^*是原问题最优解的集合,对于任意的\lambda \ge 0和任意的v,下式都是成立的:
g(\lambda, v) \le p^*这个非常容易证明
假设\bar{x}是原问题的一个最优解,即f_i(\bar{x}) \le 0且h_i(\bar{x}) = 0,根据假设\lambda \ge 0,我们有:
\sum\limits_{i=1}^{m} \lambda_i f_i (\bar{x}) + \sum\limits_{i=1}^p v_i h_i (\bar{x}) \le 0因为左边第一项是负数,第二项为0,因此,必然有:
L(\bar{x},\lambda,v) = f_0 (\bar{x}) + \sum\limits_{i=1}^{m} \lambda_i f_i (\bar{x}) + \sum\limits_{i=1}^p v_i h_i (\bar{x}) \le f_0 (\bar{x})所以:
g(\lambda,v) = \min\limits_{x} L(x,\lambda,v) \le L(\bar{x},\lambda,v) \le f_0 (\bar{x})。
4)证明:对偶函数是一个凹函数
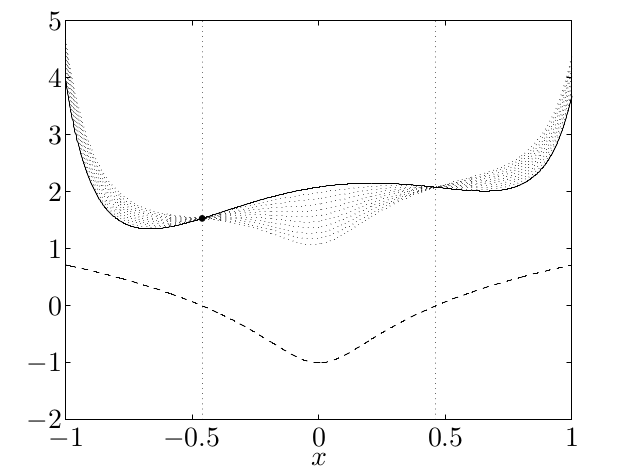
设f(x)函数满足定义:\forall x_1,x_2 \in I, 有f[(x_1 + x_2)/2] \ge \frac {f(x_1) + f(x_2)} {2}
则f(x)就是凸函数,-f(x)就是凹函数,如下图,左边是凸函数,右边是凹函数

5)证明:对偶问题是一个凸问题
6)KKT 条件
xx