最近在研究大模型的强化学习,整理下相关的算法基础,了解一下当前主流强化学习算法的一些改进思路
1. 目标函数
1.1. 预训练
自回归模型的目标是预测序列中的下一个词元,也是使用交叉熵损失:
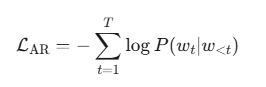
其中:
-
T 是序列长度。
-
w_t 是时间步 t 的真实词元。
-
w_{<t} 是时间步 t 之前的所有词元。
-
P(w_t | w_{<t}) 是模型预测给定历史词元后,下一个词元为 w_t 的概率。
1.2. 强化学习
最大化目标函数(最大化优势) = 最小化 -目标函数
所以强化学习把 loss 定义为 = - si(θ) * adv
(1)PPO
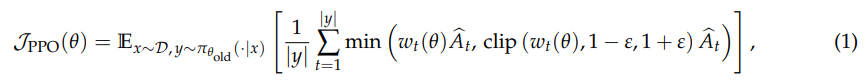
(2)GRPO
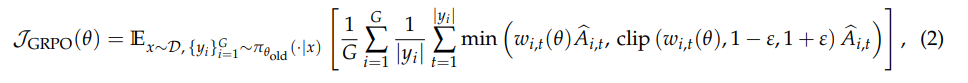
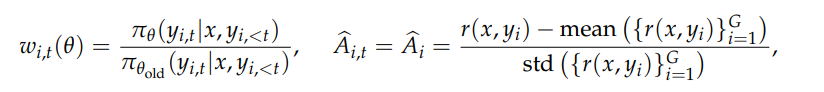
其中:
- G 表示同一个 prompt 的G条样本答案
- y_i表示第几条样本,|y_i|表示向量的长度的,也就是 token 数,但是实际上这里面loss是求平均还是求和,有很多算法:token-mean,seq-mean-token-sum,seq-sum-token-mean
GRPO 计算的是 token 粒度的平均 loss
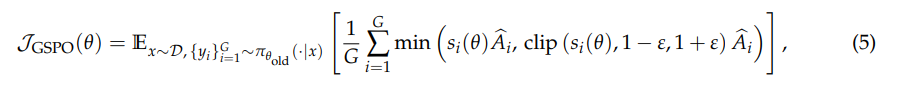
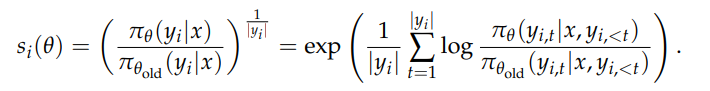
优势计算和 GRPO 一样
GSPO 计算的是 seq 粒度的平均 loss
(4)DAPO
xx
(5)BAPO
和预训练不一样,强化学习是基于 reward 而不是交叉熵,token-level-reward
2. 求导:权重是怎么更新的?
2.1. 链式法则
2.1.1. 举例:Linear
举例:
W = torch.tensor([a1, a2])
y = Wx + b
loss = (y- y’)^2 = (Wx + b – y’)^2
训练过程中,对于数据集 x
2.1.2. 举例:RL
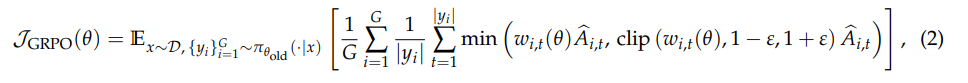
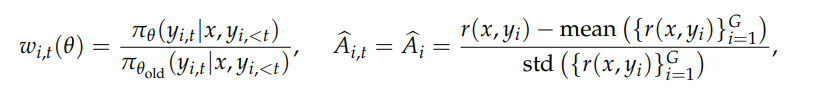
整个公式里面,其实只有\piθ是需要求导的,因为\piθ是模型的输出,也就是 \piθ = f(Wθ)。其他的\piθ_{old}不需要求梯度,\hat A也不需要求梯度
求导最终计算的是\nabla Wθ
假设我们把 clip 去掉,求导公式本质上是:
\frac{\hat A_{i,t}}{\pi_{θ_{old}}} * f'(Wθ)clip 部分的梯度单独计算并累加
2.2. 梯度累加
如果使用 x1 和 x2 放到一个batch里训练,最终的梯度等价于单独使用 x1 和 x2 来训练时的梯度累加求平均
optimizer.zero_grad()
outputs = model(torch.tensor([0, 10], dtype=torch.float))
loss1 = nn.MSELoss()(outputs.squeeze(), torch.tensor([0], dtype=torch.float))
outputs = model(torch.tensor([10, 0], dtype=torch.float))
loss2 = criterion(outputs.squeeze(), torch.tensor([0], dtype=torch.float))
loss = (loss1 + loss2) / 2
loss.backward()
optimizer.step()
print(f"模型参数: a={model.linear.weight[0,0].item():.4f}, b={model.linear.weight[0,1].item():.4f}, c={model.linear.bias[0].item():.4f}")
和下面的是等价的:
因为 nn.MSELoss() 本身就是对输出的 loss 求平均
2.3. 权重更新幅度
由2个因子决定,学习速率,梯度值
W = W - \eta \nabla W
其中\eta是一个超参,\nabla和 loss 大小正相关,loss越大,更新幅度越大,loss越小,更新幅度越小
特别注意,根据链式法则和梯度累加的原理
洞察:token之间对权重的影响都是相互独立,因为这个只跟模型和输入相关,这个计算是无法人为修改的。无论loss怎么算,都无法让B token对A token的权重更新产生影响。
但是最终loss怎么算,改变了不同token的更新幅度,导致出现了B影响A的“现象”
2.4. clip 的原理和副作用
强化学习过程中,经常会使用 clip 来限制梯度爆炸,但是一定要理解 clip 对梯度的影响
一旦某个变量被 clip 之后,token的loss就是一个常数了,根据 torch 的链式法则,该 token 对应的梯度就是 0,对权重不会产生任何更新操作。
clip 可能会存在一些副作用
1)对 GRPO
GRPO 是 token-level 粒度的 loss 计算,如果一些 token 的重要性偏差太大,被 clip 了,可能有反效果
比如 ABCDE,其中D的重要性偏差太大了,但是C,E都没有问题
权重更新的时候,D的梯度累积被丢弃,但是D、E的计算是依赖ABC的,所以这个更新可能会有bad case
2)对 GSPO
GSPO的clip是seq粒度的,所以如果被clip了,相当于整个seq不参与梯度计算,会有计算浪费。所以这个应该怎么clip,是要谨慎的
3.【重要】agg-loss
我们看到,经典的 GRPO 算法是这样的:
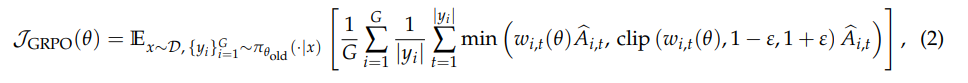
RL的目标是最大化优势,总优势就是单个token的优势“聚合”得到的,单个 token 的优势就是w_{i,t}(θ)\hat A_{i,t},但这其实是一个“线性”函数,它的偏导就是\hat A,因此它的梯度(按照链式法则)是\hat A * w'_{i,t}(θ)
grpo的默认聚合算法就是 seq-mean-token-mean,就是\frac{1}{G} \sum_{i=1}^{G} \frac{1}{|y_i|}\sum_{t=1}^{|y_i|}这一部分
3.1. agg-loss 的作用
主要作用就是2个:
-
控制总梯度
-
调节不同 token 的梯度“权重”
1)控制总梯度
如果你把 compute_policy_loss 最终计算的 loss 直接 * 2 返回,会发现梯度更新幅度直接翻倍,等价于把学习速率放大1倍
这是因为按照求导的链式法则原理,\nabla W = 2 * f'(loss)
2)调节不同 token 的梯度“权重”
agg-loss 的这个作用其实还有点隐晦,不是那么直观上容易理解
前面我们已经知道了,不同 token 对权重的贡献都是独立的,token 之间相互不影响,梯度最终会累加
那 agg-loss 的这种求平均,最后是怎么对 token 粒度的梯度产生影响的?
以 grpo 为例,根据链式法则,每个 token 的梯度都可以单独计算:
\nabla W_{i,t} = \frac{1}{G} \frac{1}{|y_i|} w_{i,t}(θ)\hat A_{i,t}
其中:
-
G:论文里写公式的时候,G都是代表每一条 prompt 的 G 条样本,一般对应 rollout.n。但是实际上 G 一般对应train_batch_size * rollout.n,每一个 step 的梯度,都是多条数据一起计算一个总loss的
-
|y_i|表示G里的第i条的seq长度
举例:
s1 = [1,1], size = 2
s2 = [0.7, 0.7, …, 0.7],size=8
最后的loss = (1+0.7) / 2 = 0.85,这是总的更新幅度
那每个 token 更新多少?对于 s2 的 token 来说,那就是 = 0.85 * \frac{0.7}{1.7}*\frac{1}{8} = 0.7 * \frac{0.85}{1.7}*\frac{1}{8}= 0.04375,也就是 0.04375 * w'_{i,t}(θ)
3.2. agg-loss 的几种聚合算法
1)token-sum
verl 其实没这个算法,但理论上这么玩也是可以的
所有token的loss直接求和,最后的效果就是每个 token 按照自己的梯度去更新权重
\nabla W_{i,t} = w_{i,t}(θ)\hat A_{i,t}
这个方式的最大问题就是,更新幅度太大了,我没跑过,但应该是会崩溃的
2)seq-mean-token-mean
前面见过了,grpo 的标准算法,单个 token 的梯度就是
\nabla W_{i,t} = \frac{1}{G} \frac{1}{|y_i|} w_{i,t}(θ)\hat A_{i,t}
3)seq-mean-token-sum
seq内token求和
seq之间求平均
那单个token的梯度就是
\nabla W_{i,t} = \frac{1}{G} w_{i,t}(θ)\hat A_{i,t}
4)seq-sum-token-mean
seq内token求平均
seq之间求和
那单个token的梯度就是
\nabla W_{i,t} = \frac{1}{|y_i|} w_{i,t}(θ)\hat A_{i,t}
我们总结一下agg-loss这几种算法的 优劣:
|
|
token 梯度 |
优势 |
劣势 |
适合场景 |
|
seq-mean-token-mean |
\nabla W_{i,t} = \frac{1}{G} \frac{1}{|y_i|} w_{i,t}(θ)\hat A_{i,t} |
|
|
|
|
seq-mean-token-sum |
\nabla W_{i,t} = \frac{1}{G} w_{i,t}(θ)\hat A_{i,t} |
|
|
|
|
seq-sum-token-mean |
\nabla W_{i,t} = \frac{1}{|y_i|} w_{i,t}(θ)\hat A_{i,t} |
|
对短seq不友好,容易梯度爆炸,因为|y_i|很小 对长文不友好,因为|y_i|很大 |
|
todo:
-
每个token的梯度,控制在什么范围内是最合适的?应该有一个经验值来指导 agg-loss 的设计
-
一个好的agg-loss应该是什么样的?
4. 重新理解一下经典RL算法的改进思路
4.1. GRPO
GRPO 最早在RL应用的论文出自 deepseek-math
ppo 主要是太复杂,了需要 critic 模型来预估状态价值和动作价值
GRPO 简化了这个逻辑,去掉了 critic 模型,使用组内相对优势 Group-based Relative Advantage
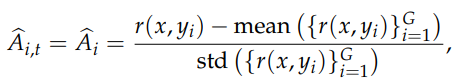
一个 prompt,根据 rollout.n 采样n次,对每个response单独打分。由于实际上无法区分每个 token 的 reward,所以实际计算时, token的reward等同于整个seq的reward
4.2. GSPO
4.2.1. 重要性采样的错误使用
阿里把 grpo 的问题描述为是一个 ill-posed problems(适定问题的定义是:解存在、必须唯一、而且稳定)
grpo 之所以有这个问题来源于对“重要性采样”的误用,这种误用会带来2个问题:
1)无法正确的修正分布
重要性采样:通过采样来估计目标策略和原有策略的分布误差,但是这个采样必须是“大量”的
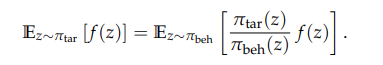
但是grpo在token粒度只有1次采样,无法起到修正分布的作用。
gspo使用seq粒度的概率分布,修正的是seq粒度的概率分布,seq粒度采样是 rollout.n,缓解了这个问题
2)高方差的梯度noise
在 grpo 算法里面
由于一个seq的所有token的adv都是一样的
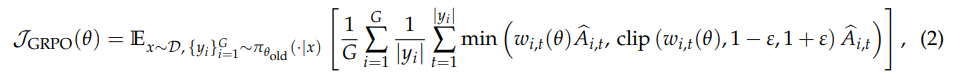
但是当句子出现乱码的时候(第一列是old_probs,第二列是 probs)
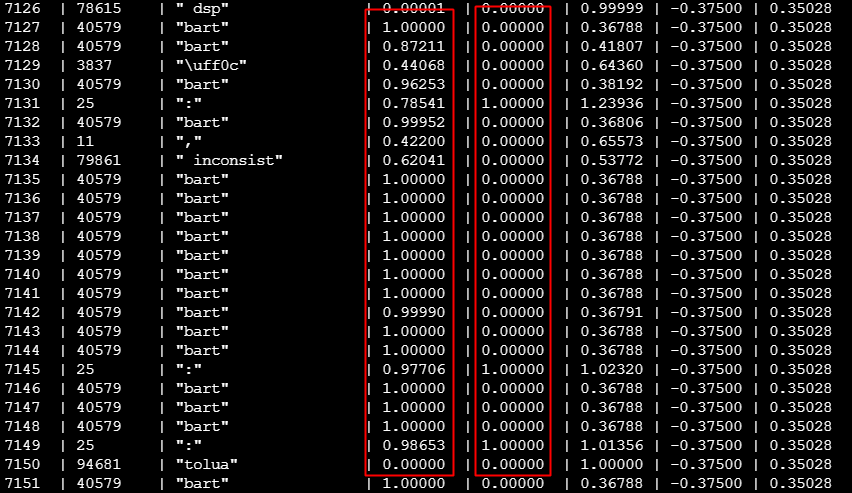
这种使用“算数平均”计算出来的优势会被放大,而 gspo 的新算法使用“几何平均”,正好可以很好的解决这种问题

gspo 能非常好的区分乱码复读机的行为
对于这种行为:
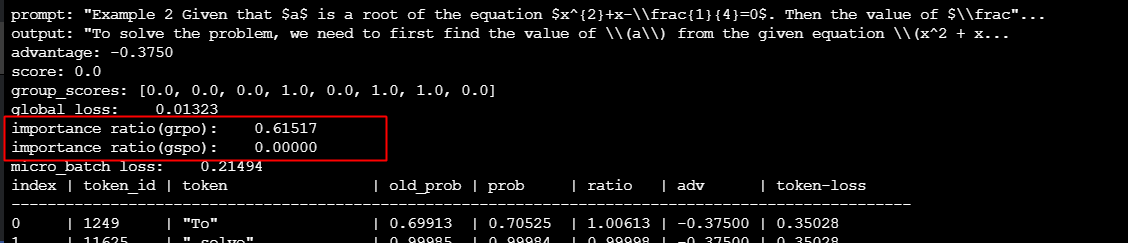
如果是正常的句子:

4.2.2. gspo 的问题
探讨下几何平均的本质问题
上述:
-
t1.mean() 就是算数平均
-
t1.log().mean().exp() 就是几何平均,对应上述算法
由于几何平均使用了乘法,当存在任意一个token的new_probs是0时,整个seq的优势都会被剔除掉。如果一个seq前面是正常的,后面是乱码,其实不应该把整个seq的重要性都置为0
4.3. DAPO
dapo 的主要优化:
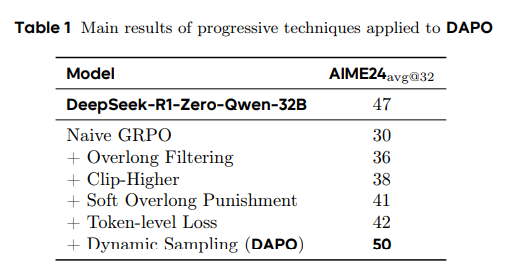
其中最重要的其实就是2个:
-
超长乘法
-
动态采样
其他的其实并不重要
4.3.1. Token-level Loss
回顾一下 grpo 的算法:
\nabla W_{i,t} = \frac{1}{G} \frac{1}{|y_i|} w_{i,t}(θ)\hat A_{i,t}
这个算法对长文不友好,因为每个 token 的梯度受自己所在的 seq 长度的限制
dapo 改进了这个算法,改成了
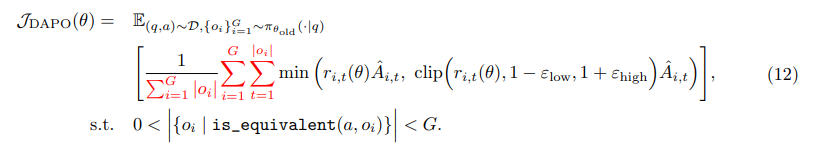
对应的 token 粒度的梯度就变成了:
\nabla W_{i,t} = \frac{1}{\sum_{i=1}^{G} {|y_i|}} w_{i,t}(θ)\hat A_{i,t}
举例:
s1 = [1,1], size = 2
s2 = [0.7, 0.7, …, 0.7],size=88
grpo:s2的token梯度是 = 1/2 * 1/88 * 0.7,s2占全体权重的 1/2
dapo:s2的token梯度是 = 1/100 * 0.7,s2占全体权重的 88/100
所以 dapo 把长文学习慢的问题解决了。
问题:有没有更好的算法?看起来学习的不够快
4.3.2. 零梯度样本:Dynamic Sampling
当一个 prompt 的所有(rollout.n)采样都是错的或者都是对的时候,这个时候大模型是学习不到任何知识的,因为这个问题的所有答案的 adv 都是 0,那对应的所有 token 的梯度也都是 0,相当于这个 prompt 的所有 token,梯度更新的时候不会对权重做任何更新
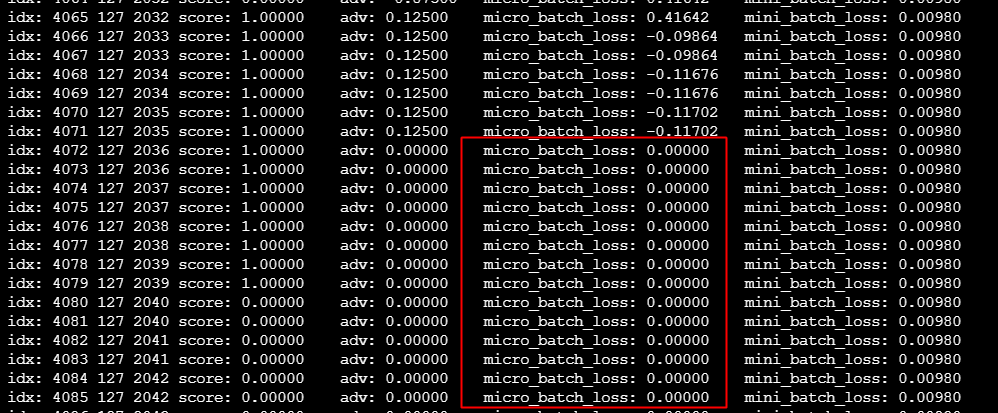
以之前 gsm8k + qwen-7b 的模型为例,大概有高达16%的采样是无效的,这个极大的影响了模型学习的速度
dapo 的解决方案:确保每个问题都有对错的答案,如果一个问题全错或者全对,那就丢弃部分数据,继续执行 rollout。虽然看起来是增大了计算量,但是实际上由于训练效率的提升,整体计算量是降低的
4.3.3. 长文惩罚
Overlong FIltering
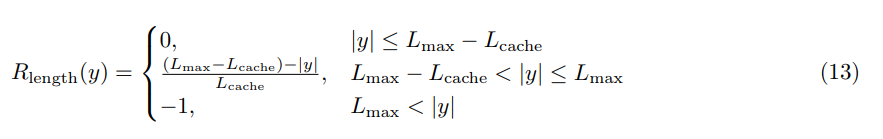
让模型学会不要太长输出的最简单的手段,就是奖励所有正确的短输出。这个操作本质上是让模型倾向于选择最终能快速到达结束符的 token
4.4. BAPO
4.4.1. 正负样本失衡问题
bapo 发现训练过程中,负样本太多,导致正样本对梯度的贡献被抑制了
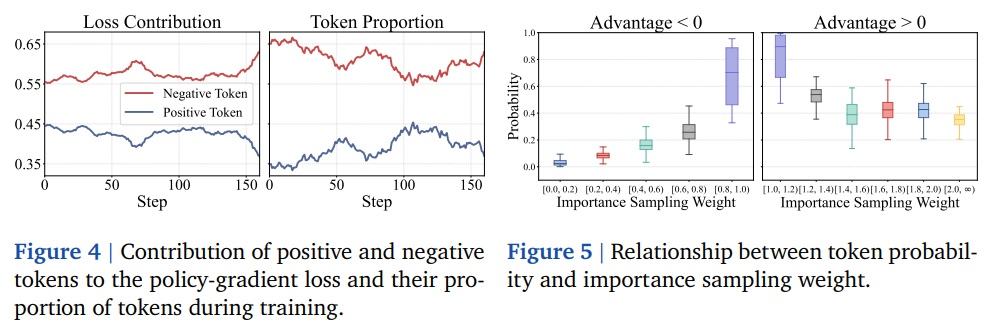
通过动态调整 clip 的上下限,为维持正样本对梯度的贡献度
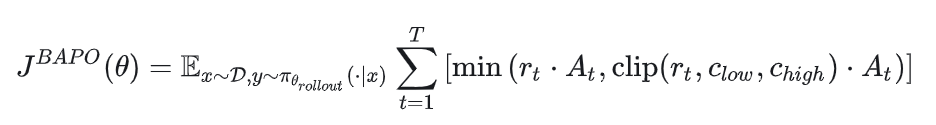
让正负样本的梯度贡献度维持在下面的比例:
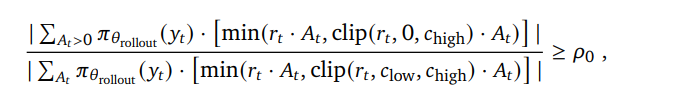
其中 Po 默认值是 0.4,也就是正样本比例对梯度的贡献至少要大于 40%
正负样本失衡,最直观的例子就是:
s1:AAABBBBBBB reward=1
s2:AAACCCCCCCC reward=0
s3:AAADDDDDDDD reward=0
对于 token AAA 来说,最终概率被弱化了(因为s2+s3产生的副作用要大于s1的正作用)