原文:https://zhuanlan.zhihu.com/p/79030485
从事分布式深度学习相关工作的同学,应该都频繁地用到了AllReduce(规约)操作。
但是对于训练框架中集成的AllReduce相关操作,其背后实现的原理是什么?
除了最近几年名声大噪的Ring AllReduce是否还有其他的AllReduce算法?
他们各自的性能开销如何?如何取舍?
本文尝试从一个较为全面的角度来展现AllReduce算法的前世今生,既分析经典算法,也介绍发展中的新秀。
MPI中的AllReduce算法
其实说到AllReduce,很多人脑海里的第一反应都是MPI_AllReduce。作为集合通信中的元老,和高性能计算领域的通信标准,在MPI_AllReduce这个通信原语背后,MPI中实现了多种AllReduce算法。
以openMPI源码为例,里面实现了多种allreduce的算法。具体的算法选择在
ompi/mca/coll/tuned/coll_tuned_decision_fixed.c

reduce+broadcast
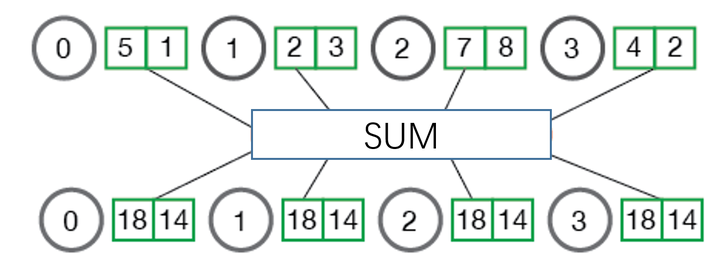
这是最朴素最直观的一种算法(也是经典的PS架构对应的算法)。如图3所示,parameter server作为中心节点,先全局reduce接收所有其他节点的数据,经过本地计算后,再broadcast回所有其他节点。其中实线表示真实发生了的通信;而虚线表示只是示意,并没有实际通信。
对于耗时的估计,本文都按照公式α + S / B + S * C来计算。
其中α表示2个通信节点(这里节点不指机器节点,而是指集合通信中的一个node,比如1个mpi process即可认为是一个通信节点)间的latency, S(ize)表示要allreduce的数据块大小, B(andwidth)表示2个通信节点间的带宽, C(omputation)表示每字节数据的计算耗时。另外以N(umber)表示节点个数。

通信只需要2步,一步reduce,一步broadcast。它们的通信耗时都是α + S / B。(abc与d之间的通信是同时进行的,耗时只算1份)
在parameter server节点上的计算耗时是N*S*C。
总体耗时是2*(α + S/B) + N*S*C。
该算法最大的缺点就是parameter server节点的带宽会成为瓶颈。
也许有人会质疑说可以用分布式PS,PS集群的带宽就足够大了。
分两种情况,如果是数据并行,那分布式PS之间的权重协调一致将是不得不考虑的问题;如果是模型并行,那对于某一块特定的参数来说,PS:worker都是1:N的关系,当worker数量较大时,还是不可避免遇到PS的带宽瓶颈。
recursive halving and doubling
可以视为经典的树形算法,过程也非常直白。
如果节点数是2的幂,所需通信步数是2*log2N。
下图是4个节点abcd进行recursive halving and doubling的allreduce示意图。其中实线表示真实发生了的通信;而虚线表示只是示意,并没有实际通信。
相比reduce+broadcast,最大的改进是规避了单节点的带宽瓶颈。

图4 recursive算法示意图,节点数为2的幂
如果节点数不为2的幂,则会先调整至符合2的幂后,再进行上述halving and doubling的操作。总的通信步数是2*( log2K+1)

在halving和doubling的每一步,通信耗时都是α + S/B,计算耗时都是S*C。
步数约等于log2N,因此整体耗时是2*log2N*(α + S/B + S*C )。
Butterfly
Recursive算法中一个明显的不足是,在halving阶段有一半的节点没有进行send发送操作,只是“傻傻”等待接收数据。比如图4中的第一步,a->b,c->d发送数据的时候,b和d节点的发送带宽没有被利用起来。
Butterfly算法则弥补了这一点。通信的每步中,所有节点的send和recv带宽都被利用起来了。
这个算法在openMPI中对应mca/coll/base/coll_base_allreduce.c中的ompi_coll_base_allreduce_intra_recursivedoubling函数(对,别被函数名字骗了,它实现的不是上面介绍的recursive算法)。
如果节点数是2的幂,所需通信步数只要log2N。
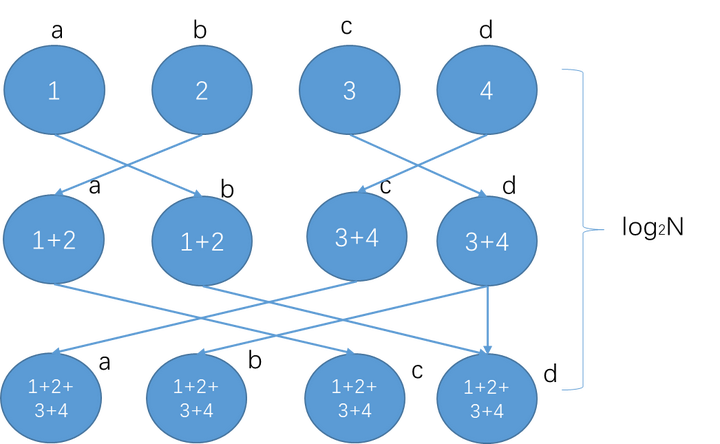
图6 Butterfly算法示意图,节点数是2的幂(是不是有点蝴蝶的形状?)
如果节点数不为2的幂,也是先调整为符合2的幂后,再进行上述操作。总的通信步数是log2K+1。
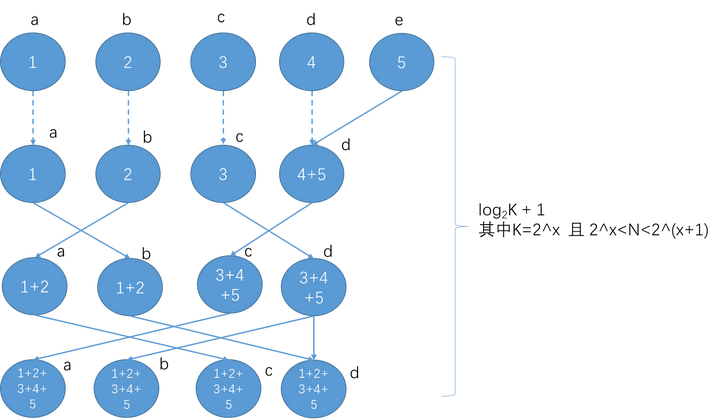
通信步数大概是log2N, 每步的通信耗时是α + S/B,计算耗时是S*C。
整体耗时大概是log2N*(α + S/B + S*C )。
Ring AllReduce
Butterfly已经在每步中把每个节点的send/recv带宽都利用起来了,那是不是完美无缺了?答案是否定的。其潜在的问题是如果数据块过大(S过大),每次都完整send/recv一个S的数据块,并不容易把带宽跑满,且容易出现延时抖动。
Ring算法默认把每个节点的数据切分成N份。当然,这要求数据块中的元素个数count =S/sizeof(element)大于N,否则要退化为使用其他算法。
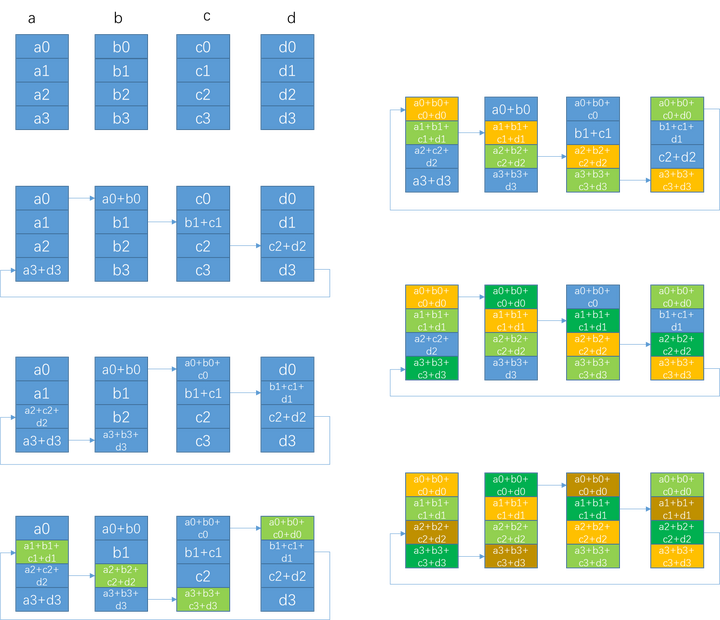
图8 Ring Allreduce算法示意图
第一阶段通过(N-1)步,让每个节点都得到1/N的完整数据块。每一步的通信耗时是α+S/(NB),计算耗时是(S/N)*C。 这一阶段也可视为scatter-reduce。
第二阶段通过(N-1)步,让所有节点的每个1/N数据块都变得完整。每一步的通信耗时也是α+S/(NB),没有计算。这一阶段也可视为allgather。
整体耗时大概是2*(N-1)*[α+S/(NB)] + (N-1)*[(S/N)*C]
Segmented Ring算法
主要是针对较大数据量的情况下,直接按照进程数来切分数据,可能导致单次要传输的数据依然过大,影响性能。所以改成分段执行ring。
其所需步数以及耗时和选定的切分size大小有关。切分后的过程和ring类似,此处不再赘述。
MPI中选择AllReduce算法的逻辑
我们何时该选择哪种算法呢?不妨看下openMPI里是怎么帮用户做选择的。
对照图2中的代码片段,其算法选择逻辑如下

2015年NCCL开始实现AllReduce
上述openMPI的算法最晚在2009年就都已经成熟并开源了,而英伟达在2015年下半年首次公开发布NCCL。
既然openmpi已经实现了这么多AllReduce算法,为什么英伟达还要开发NCCL?
从openMPI的源码里我们能看到,其完全没有考虑过深度学习的场景,基本没有考虑过GPU系统架构。很明显的一点,MPI中各个工作节点基本视为等同,并没有考虑节点间latency和带宽的不同,所以并不能充分发挥异构场景下的硬件性能。
而NCCL的优势就在于完全贴合英伟达自己的硬件,能充分发挥性能。但是基本的算法原理其实相比openmpi里实现的ring算法是没有变化的。
NCCL1.x只能在单机内部进行通信,NCCL2.0开始支持多节点(2017年Q2)。所以在NCCL2之前大家还会依赖MPI来进行集合通信。
2016年百度在深度学习中引入Ring AllReduce
openMPI代码中2007年就有ring算法了,为什么会有Baidu在2016年提出Ring Allreduce的说法?
其实在baidu的论文题目里就说得很清楚了,他们是“Bringing HPC Techniques to Deep Learning”,ring算法是早就有了,但是应用到深度学习领域确实是他们首创的(所以跨领域跨学科的复合型人才是多么重要^_^)。
Baidu还开源了他们基于TensorFlow修改的源码,把TF里原来进行梯度规约的地方替换成了mpi实现的ring allreduce。
具体代码在tensorflow/contrib/mpi_collectives/ring.h中
可以看到实现的是常规ring,而不是segmented ring。并且里面使用MPI_Sendrecv MPI_Irecv MPI_Send这些mpi通信原语来实现,和具体mpi库无关(无论是openmpi还是MPICH2)。也没有直接用MPI_AllReduce原语,因为按照openMPI的实现它很可能跑去用其它非ring算法了。
TensorFlow里的AllReduce
在tf早期版本中,分布式训练只有PS架构。
在2017年后,开始逐步支持多种allreduce算法,其中的ring-allreduce实现正是baidu贡献的。
NCCL2.0之后,TensorFlow/Baidu里的allreduce算法集成了NCCL来做GPU间通信,而不是依赖MPI了。
MPI和NCCL的关系
是不是从此我们只要NCCL,不再需要MPI了呢?NO
Nvidia的策略还是比较聪明,不和MPI竞争,只结合硬件做MPI没做好的通信性能优化。在多机多卡分布式训练中,MPI还是广泛用来做节点管理。当红炸子鸡Horovod也是这么做的,NCCL只做实际的规约通信。

Ring算法的问题
Ring算法是不是就完美无缺了呢?显然不是,因为虽然它可以充分利用带宽,但非常遗憾的是随着节点数的增多,单个ring越来越庞大,延迟将不可接受。
这也带来了各种改良的Ring算法。
改良Ring算法
2018年下半年机智团队提出分层Ring AllReduce

也是2D的一种形式,组内reduce->组间allreduce->组内broadcast,这种方法意在充分利用组内的高带宽的同时,弱化组间的低网络带宽带来的影响。
第一阶段reduce的通信步数是1,通信耗时是α + S / B,计算耗时n*S*C。其中n是我们分的每组内的节点数(这里是GPU卡数),当时设置的是每组16卡。
第二阶段allreduce的整体耗时套用前面的公式,是2*(m-1)*[α+S/(mB)] + (m-1)*[(S/m)*C]。其中m是我们第二层的节点数(也就是我们分的组数)。
第三阶段broadcast的通信步数是1,通信耗时是α + S / B,没有计算。
整体耗时是2*(α+S/B)+n*S*C+2*(m-1)*[α+S/(mB)] + (m-1)*[(S/m)*C]。
2018年11月索尼公司提出2D-Torus算法
该算法的论文直到2019年5月一直在修改中,其主要思想也是分层,是组内scatter-reduce->组间allreduce->组内allgather。

第一阶段scatter-reduce通信步数n-1,每一步的通信耗时是α+S/(nB),计算耗时是(S/n)*C。 第二阶段allreduce整体耗时套用前面的公式,是2*(m-1)*[α+S/(mB)] + (m-1)*[(S/m)*C]。其中m是第二层的节点数(也就是分的组数)。
第三阶段allgather通信步数n-1,每一步通信耗时也是α+S/(nB),没有计算。
整体耗时大概是
2*(n-1)*[α+S/(nB)] + (n-1)*[(S/n)*C] + 2*(m-1)*[α+S/(mB)] + (m-1)*[(S/m)*C]
2018年12月谷歌提出2D-Mesh算法
主要思想还是分层,并且和索尼2D-Torus很类似,都是水平和垂直两个方向,但是其步骤更简单。
第一步的水平和垂直两个方向的ring,并没有做reduce-scatter,而是最简单的转2圈来完成。通信步数分别是n-1和m-1(水平和垂直方向同时执行,m是行数,n是列数),每一步的通信耗时是α+S/B,计算耗时是S*C。总体耗时是(m+n-2)*( α+S/B+S*C)。
第二步则换方向,在垂直和水平两个方向,继续转2圈来完成。耗时同样是(m+n-2)*( α+S/B+S*C)。
整个算法耗时是2*(m+n-2)*( α+S/B+S*C)。
为什么谷歌的2D-Mesh可以比上述2D-Torus更简洁和高效?关键原因在于使用的TPU节点可以同时进行2路send和2路recv,而我们普通的服务器都是只有一张网卡,只能同时进行1路send和1路recv。
这也是谷歌论文里可以说自己的网络通信次数从传统Ring的O(N2)降低到了O(N)。


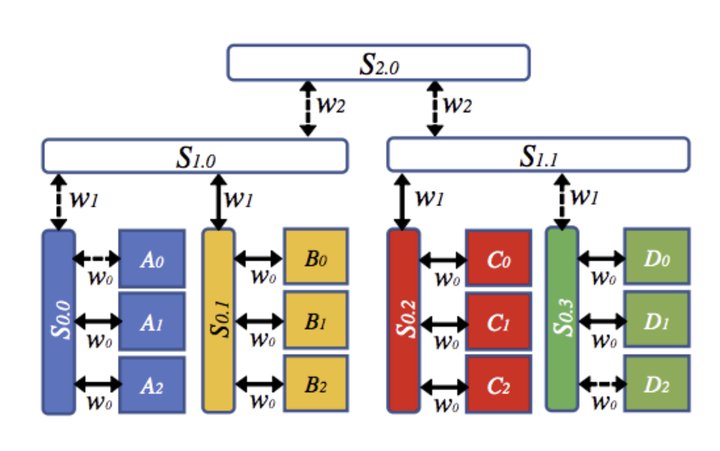
2018年7月IBM提出3D-Torus算法
IBM提出的名为BlueConnect的算法,比上述2D算法更进一步,形成了3个维度上的分解,因此可以归类为3D-Torus算法。
其主要思想是考虑了节点间不同switch的带宽不同,从而做出不同的分解。
以图15为例,里面同色的节点间以S0.0/S0.1/S0.2/S0.3这些switch相连,带宽是w0;
S0.X的switch和上一层switch S1.0/S1.1之间带宽是w1;
S1.X的switch和顶层的switch S2.0之间带宽是w2。
Step1:在节点内(同一个S0.X的switch下,带宽w0)同时执行四个reduce-scatter操作(A0-A1-A2, B0-B1-B2,C0-C1-C2, D0-D1-D2)。
Step2:在节点间(同一个S1.X的switch下,带宽w1)同时执行六个reduce-scatter操作(A0-B0, A1-B1, A2-B2,C0- D0, C1-D1, C2-D2)。 A {0,1,2}→B {0,1,2}在S1.0上运行,C {0,1,2}→D {0,1,2}在S1.1上运行,所有这些都同时发生,共享S1.x带宽。
Step3:在节点间同时执行六个reduce-scatter操作(A0-C0, A1-C1, A2-C2,B0- D0, B1-D1, B2-D2),同时在S2.0上共享S1.x带宽。Step3后每个GPU上有S(ize)/12的数据是完成所有ReduceScatter后完整的数据,此时完成所有reduce-scatter操作。
Step4:all-gather将以完全相同但相反的顺序执行,最终完成all-reduce。
此种方法考虑到了一般机房内的3层拓扑结构(机器内->机器间交换机->上层交换机/路由器),不过其性能理论上和w0/w1/w2以及节点数N息息相关,不同取值情况下其与上述2D算法的性能优劣对比有很大不同,本文不再详细分析阐述。

2019年上半年NCCL2.4提出double binary tree算法
其主要思想是利用二叉树中大约一半节点是叶子节点的特性,通过将叶子节点变换为非叶子节点,得到两颗二叉树,每个节点在其中一颗二叉树上是叶子节点,在另一颗二叉树上是非叶子节点。
这种方法理论上是能够提供比ring算法更低的延迟(log2N < N),但实际效果需要测试。后续机智团队在资源条件合适的情况下会安排进行对比。
各种AllReduce算法对比

以上对各种经典的和新提出的AllReduce算法进行了一些介绍和分析,如有纰漏欢迎交流和批评指正。
值得一提的是,上述介绍的经典ring-allreduce、分层ringallreduce都是机智团队实际应用到业务中并取得了较好效果的算法。欢迎有兴趣的同学加入,一起探索。
参考资料
[1]:https://github.com/open-mpi/ompi/issues/4067
[2]: https://devblogs.nvidia.com/massively-scale-deep-learning-training-nccl-2-4
[4]: http://andrew.gibiansky.com/blog/machine-learning/baidu-allreduce/
[5]: https://nnabla.org/paper/imagenet_in_224sec.pdf
[6]: http://www2.cs.uh.edu/~gabriel/courses/cosc6374_f07/ParCo_18_PerformanceModeling_2.pdf
[8]:Massively Distributed SGD: ImageNet/ResNet-50 Training in a Flash
[9]:Image Classification at Supercomputer Scale
[10]:公司内部分资料