参考 mit 课程：https://web.mit.edu/6.034/wwwbob/svm.pdf

SVM 是机器学习领域非常流行的一个分类算法。他的前身其实就是感知机，想了解感知机原理的可以简单看我之前写的文章

传统感知机是有很多局限性的问题的，比如解决不了线性不可分的问题，比如泛化能力不强因为你可以找到N个解，但是不知道哪一个是最好的。SVM 就能很好的解决这些问题。

1. 支持向量

搞清楚什么是支持向量是了解SVM的前提。但是这里只能抽象的讲解，了解后面的内容，会加深你对支持向量的理解

在一个分类问题里，我们可能会有多个解，比如：

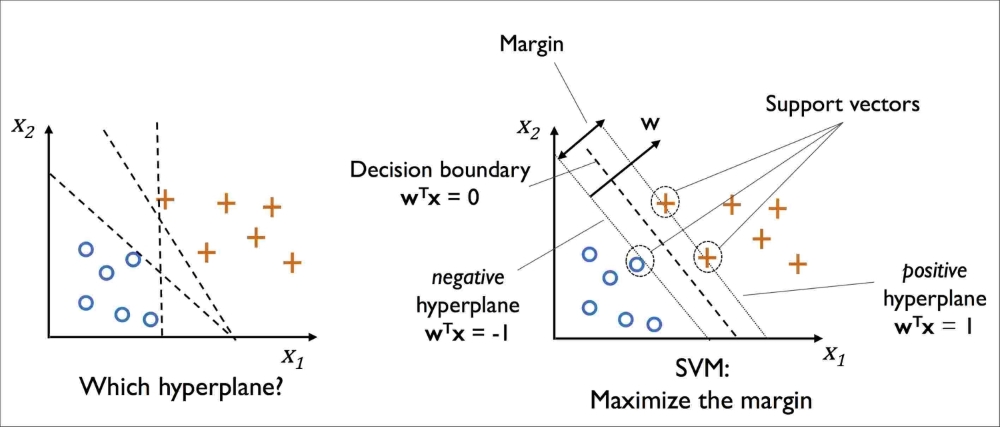
但是取哪个是最好的呢？直觉告诉我们，选能让样本分割的最远的超平面，这个就是 SVM 的做法，最大间隔化（后面会讲形式化的定义和推导）。SVM使用两个间隔最大的超平面，将所有数据完美分割在两边。

所以数学上，只需要一个超平面 + 间隔，就能形成一个决策边界，那些依附在决策边界上的点，就叫支持向量。为什么要给这些点起一个专有的名词？因为定义这个超平面只需要用到这些点，而其他远距离的点都是多余的。所以通常在一个2维空间上，最少只需要3个点，就能定义这个超平面

备注：超过3维空间的决策平面不好描述

2. SVM 的目标函数

SVM 的目标就是最大化数据点（支持向量，也就是离超平面最近的点）到超平面的间隔。数学上形式化的定义是：

这个函数 min 是找到那些函数间隔最小的点，其实讲的就是支持向量。但是支持向量和超平面是息息相关的，不同的超平面有着不同的支持向量。比如在一个样本数据集里面，我们也许可能会找到N个超平面以及（决定）这个超平面的的支持向量。最终，我们会选择支持向量到超平面最大的一个，也就是 max

我们稍微转化一下，把求最小值部分，放到约束条件里面去，这样就可以得到

，其中

st.

这个就是 SVM 的目标函数

网上几乎所有的资料，包括mit的讲义，甚至是西瓜书，在讲 SVM 目标函数的时候，都是直接导出这个公式，其实这是很不严谨的，我一开始学习的时候，为了搞清楚这个地方也花费了不少时间

为什么从能直接推导到，或者说，对于求解SVM模型参数最优解的情况下，这两个目标函数是等价的，这是为什么？

这里我们要讲一下函数间隔和几何间隔

前面我们讲的目标函数，其自身求的是几何间隔，而目标函数的分子一项 是函数间隔(Functional Margin)

函数间隔有一个比较有意思的地方就是，等比缩放函数中的每一项，不会改变超平面的位置。例如对于位于三维空间中的二维平面 , , ，我们扩大或者缩小 和 并不会影响平面，即 与原始平面相同。

所以对于原目标函数，如果我们将所有参数 和 除以 ，便有

于是有:

arg \underbrace{min}_{w,b} \frac{1}{||w||}

st. y_i * (wx_{i}^T + b) \ge 1, i = 1,2,..., k

就得到了现在大家最常见的目标函数

3. SVM 的拉格朗日对偶

所谓拉格朗日对偶，的意思是，通过拉个朗日算法，将一个带约束的优化问题转化成无约束的优化问题，再求他的对偶（进一步简化）

我们上面的目标函数是在求最大值，我们再继续转换一下，转成求最小值

arg \underbrace{min}_{w,b} \frac{1}{2}||w||^2 \\ st. \\ 1 - y_i(wx_{i}^T + b) \le 0, i = 1,2,...,k

这是 一个突函数，原本很容易求解。但是带着一个优化约束，就很复杂了。这个时候拉格朗日乘数法就派上用场了

在数学最优问题中，拉格朗日乘数法（以数学家约瑟夫·路易斯·拉格朗日命名）是一种寻找变量受一个或多个条件所限制的多元函数的极值的方法。这种方法将一个有n 个变量与k 个约束条件的最优化问题转换为一个有n + k个变量的方程组的极值问题，其变量不受任何约束

因此，我们可以通过拉格朗日函数将我们的优化目标转化为无约束的优化函数：

L(w,b,\alpha) = \frac{1}{2}||w||_2^2 - \sum\limits_{i=1}^{m}\alpha_i[y_i(w^Tx_i + b) - 1] \\ st. \alpha_i \geq 0

由于引入了朗格朗日乘子，我们的优化目标变成：\underbrace{min}_{w,b}\; \underbrace{max}_{\alpha_i \geq 0} L(w,b,\alpha)

进一步转化成拉格朗日对偶形式：\underbrace{max}_{\alpha_i \geq 0} \; \underbrace{min}_{w,b} L(w,b,\alpha)

从这个公式里，我们可以先求优化函数对于w和b的极小值。接着再求拉格朗日乘子$\alpha$的极大值。

\underbrace{min}_{w,b} L(w,b,\alpha) 这个我们通过求偏导即可求解

\frac{\partial L}{\partial w} = 0 \;\Rightarrow w = \sum\limits_{i=1}^{m}\alpha_iy_ix_i \\ \frac{\partial L}{\partial b} = 0 \;\Rightarrow \sum\limits_{i=1}^{m}\alpha_iy_i = 0

把这两个公式代入原目标函数，一步一步推导，即可得到（省略推导过程，自己手写）

\begin{aligned}\underbrace{min}_{w,b} L(w,b,\alpha) = \frac{1}{2}||w||_2^2 - \sum\limits_{i=1}^{m}\alpha_i[y_i(w^Tx_i + b) - 1] \\ = \frac{1}{2}w^T\sum\limits_{i=1}^{m}\alpha_iy_ix_i - w^T\sum\limits_{i=1}^{m}\alpha_iy_ix_i - \sum\limits_{i=1}^{m}\alpha_iy_ib + \sum\limits_{i=1}^{m}\alpha_i \\ = - \frac{1}{2}w^T\sum\limits_{i=1}^{m}\alpha_iy_ix_i - \sum\limits_{i=1}^{m}\alpha_iy_ib + \sum\limits_{i=1}^{m}\alpha_i \\ = \sum\limits_{i=1}^{m}\alpha_i - \frac{1}{2}\sum\limits_{i=1,j=1}^{m}\alpha_i\alpha_jy_iy_jx_i^Tx_j \end{aligned}

这个就是 \underbrace{min}_{w,b} L(w,b,\alpha) 的求解过程，我们可以看到，最终的公式里面，最小值只和 α 相关，因为w和b的偏导就只有α因子。

最后，只需要求得 \underbrace{max}_{\alpha_i \geq 0} \;  L(w,b,\alpha)，即可得到最终的w,b值

\underbrace{max}_{\alpha} -\frac{1}{2}\sum\limits_{i=1}^{m}\sum\limits_{j=1}^{m}\alpha_i\alpha_jy_iy_j(x_i \bullet x_j) + \sum\limits_{i=1}^{m} \alpha_i \\ s.t. \; \sum\limits_{i=1}^{m}\alpha_iy_i = 0 \\ \alpha_i \geq 0 \; i=1,2,...m

由于 α 的求解涉及到 SMO 算法，目前还不太了解，暂且跳过，后续研究一下

到目前为止，SVM 目标函数的推导就基本完成了