线性回归：2 – 2 – Cost Function (8 min).mkv

逻辑回归：6 – 4 – Cost Function (11 min).mkv

在看吴恩达的机器学习教程时，逻辑回归的代价函数怎么来的一开始没看懂，后来想了一下想明白了，记录一下

我们都知道，线性回归（不管是单变量还是多变量）

它的代价函数就是均方误差，这个很容易理解。如果是单变量线性回归，那就是 J(\theta_0,\theta_1) = \frac {1} {2m} \sum_{i=1}^{m} (h_{\theta}(x^{(i)}) - y^{(i)})^2，把这个函数绘制成一个等高线图，就是这个样子的，这是一个典型的凸函数，必然能够找到一个最小值

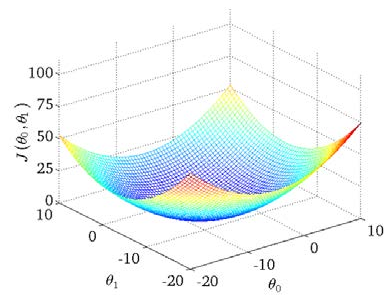
但是逻辑回归模型，不是这样的。逻辑回归模型里面，输入一组样本，输出只有0-1两种值。是一个非线性函数

当我们将

h_{\theta} (x) = \frac {1} {1 + e^{-\theta^Tx}}

代入均方误差公式时，得到的代价函数将是一个非凸函数（non-convexfunction），这个函数是这样的，用梯度下降算法没法找到一个最优解

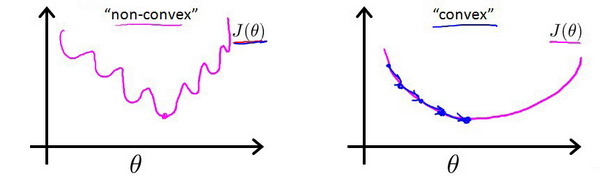
所以我们必须找到一个可替代这个成本函数的另外一个函数，让我们至少能够找到一个局部最优解。

这个函数至少要能做到：当实际的 𝑦 = 1 且 ℎ𝜃(𝑥) 也为 1 时误差为 0，当 𝑦 = 1 但 ℎ𝜃 (𝑥) 不为1 时误差随着 ℎ𝜃 (𝑥) 变小而变大；当实际的 𝑦 = 0 且 ℎ𝜃(𝑥) 也为 0 时代价为 0，当 𝑦 = 0 但 ℎ𝜃(𝑥) 不为 0 时误差随着 ℎ𝜃 (𝑥) 的变大而变大

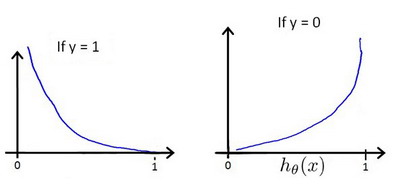
这样才符合我们对逻辑回归的直觉

所以，仔细想一下，就得到了我们想要的一个代价函数：

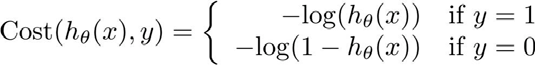
没错，这个代价函数，是找出来的，不是推导出来。后续进一步展开和简化，可参考：http://ai-start.com/ml2014/html/week3.html