nn.Linear 定义:https://pytorch.org/docs/stable/generated/torch.nn.Linear.html#torch.nn.Linear
class torch.nn.Linear(in_features: int, out_features: int, bias: bool = True)
其中:
- in_features – 每次输入的样本数,默认是1
- out_features – 每次输出的样本数,默认也是1
- bias – If set to
False, the layer will not learn an additive bias. Default:True
pytorch 本身是没有神经网络层的概念的,所以如果我们要定义一个神经网络,需要通过 torch.nn.Module 来实现
假设我们有很多样本数据,符合模型 y = wx + c,我们也可以用 torch 来直接生成一些随即样本数据
x = torch.unsqueeze(torch.linspace(0, 1, 300),dim=1)
y = 2 * x + torch.rand(x.size())
可以得到:
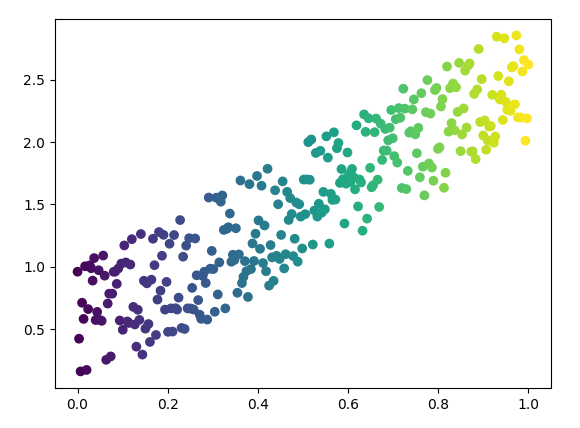
现在,我们要基于这些样本数据,反推模型 y = wx + c 中的参数 w 和 c,怎么用 torch.nn.Linear 来实现呢?
对于神经网络的典型处理如下所示:
- 定义网络结构,并构造前向网络
- 定义优化算法
- 定义损失函数 loss function
- 循环迭代,直到求解最优解
1)定义网络结构,并构造前向网络
神经网络的定义主要是层的定义,以及如何构造(前向 forward 函数)
下面这是一个单层的神经网络模型
class LinearRegression(torch.nn.Module):
"""
Linear Regressoin Module, the input features and output
features are defaults both 1
"""
def __init__(self):
super().__init__()
self.linear = torch.nn.Linear(1, 1)
def forward(self, x):
y = self.linear(x)
return y
net = LinearRegression()也可以定义多层的,对于求解简单线性回归问题,单层网络足够了
class LinearRegression(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.hidden = torch.nn.Linear(1, 10) # hidden layer
self.linear = torch.nn.Linear(10, 1) # output layer
def forward(self, x):
x = F.relu(self.hidden(x)) # activation function for hidden layer
y = self.linear(x) # linear output
return y
net = LinearRegression()2)定义优化算法
深度神经网络的优化算法有很多,比如 SGD,Adam,Adagrad 等等。但是最常用的应该还是 SGD 随即梯度下降,Stochastic Gradient Descent,pytorch 有现成的 SGD 算法可以用
class torch.optim.SGD(params, lr=<required parameter>, momentum=0, dampening=0, weight_decay=0, nesterov=False)
其中:
- params (iterable) – 待优化的参数列表
- lr (float) – 学习速率
- momentum (float, optional) – momentum factor (default: 0)
- weight_decay (float, optional) – weight decay (L2 penalty) (default: 0)
- dampening (float, optional) – dampening for momentum (default: 0)
- nesterov (bool, optional) – enables Nesterov momentum (default: False)
大多时候只会用到前面两个参数:
optimizer = torch.optim.SGD(net.parameters(), lr=0.001)另外学习速率这个参数需要注意一下,学习速率太快,可能会导致模型无法收敛,学习速度太慢,性能会很差。其实可以动态的设置学习速率,随着收敛程度越大,逐渐降低学习速率
3)定义损失函数 loss function
损失函数的是整个优化过程的目标,当误差优化到一定程度之内,学习过程就可以结束了。最常见的损失函数就是 MSE – 均方误差
class torch.nn.MSELoss(size_average=None, reduce=None, reduction: str = ‘mean’)
看了一下官方文档:https://pytorch.org/docs/stable/generated/torch.nn.MSELoss.html#torch.nn.MSELoss
size_average 和 reduce 都是废弃参数了,之看 reduction 即可
reduction (string, optional) – Specifies the reduction to apply to the output: 'none' | 'mean' | 'sum'. 'none': no reduction will be applied, 'mean': the sum of the output will be divided by the number of elements in the output, 'sum': the output will be summed. Note: size_average and reduce are in the process of being deprecated, and in the meantime, specifying either of those two args will override reduction. Default: 'mean'
loss_function = torch.nn.MSELoss()4)循环迭代,求最优解
整个迭代的过程非常简单:
- 处理数据集
- 计算 loss
- 反向传播求梯度
- 根据梯度改变参数值
for epoch in range(1000):
prediction = net(x)
loss = loss_function(prediction, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()反向传播的过程只需要调用loss.backgrad()函数即可。但是由于变量的梯度是累加的,所以在求backward之前应该先对现有的梯度清零
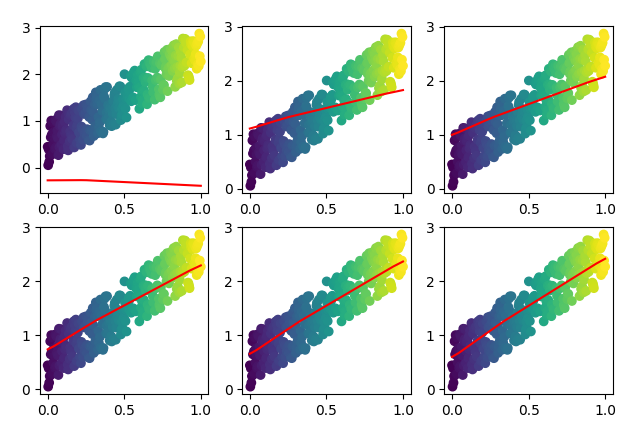
如果把求解过程可视化的话,最终看起来是这个样子的