很多时候我们有一堆数据，并且也知道数据的基本模型，但是不知道模型的参数是什么。这是基本的机器学习过程，这个过程就叫参数估计

比如我们现在就有一堆数据，模型是y = \beta_0 x + \beta_1 + \xi = \beta^T X + \xi，我们要求\beta

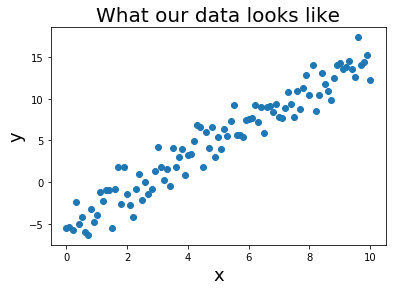
常见的计算\beta的手段有：

1. 最小二乘法
2. 最大似然估计
3. 最大后验估计
4. 贝叶斯估计

但是这几种估算方法的背后，其实代表了两类学术派别，也就是大家学习贝叶斯的时候经常听到的，频率学派和贝叶斯学派

今天来捋捋这两种学派的区别和联系

1. 频率学派

在频率派学者的认知中，当时间发生的次数趋于无穷大时，事件发生的概率就会趋于真实的理论值，这潜意识里暗含着概率是一个定值，只是未知而已。所以频率派要做的事情就是从大量随机的样本数据中，找到最接近的参数值

比如最小二乘法和最大似然估计

1.1. 最小二乘法

最小二乘法是数学家高斯在预测行星轨道时提出的。它的核心思想是：构造误差平方和函数（RSS），对其求偏导，让误差平方和函数取得最小值的参数就是模型参数

RSS = \sum_{i=1}^{m} (y - \hat{y})^2 = \sum_{i=1}^{m} (y_i - \beta^T x_i)^2

由于(y_i,x_i)是样本数据，公式中就只有一个\beta变量，所以残差RSS(\beta)就变成了关于\beta变量的函数

让残差最小，就得出了最终的参数\beta

这看起来很简单，而且听起来也似乎是正确的。我们都知道 1+1 一定等于 2

1.2. 最大似然估计

前面我们已经讲过最大似然估计。简单来说，最大似然估计的目的就是：利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值

样本数据的联合概率如下：

\hat \theta_{ML} (x) = \mathop{\arg\max}_{\theta} p(x|\beta) = \mathop{\arg\max}_{\theta} \prod_{i=1}^{n} p(x_i|\beta)

让p(x|\beta)联合概率最大，就得到了\beta的解

那p(x|\beta)是什么呢？样本数据在参数\beta下的概率，怎么定义？

因为误差一定是服从正态分布的，所以说，在\beta已知的情况下，任意的样本数据x_i,y_i必然也服从正态分布：

1. 任意的x_i，其y_i取值符合正态分布
2. 任意的y_i，其x_i取值符合正态分布

p(x,y) = \frac {1}{\sqrt{2\pi}\sigma} exp(-\frac {(y - \theta x)^2}{2\sigma^2})

所以：

\prod_{i=1}^{n} p(x_i|\beta) = \prod_{i=1}^{m} \frac {1}{\sqrt{2\pi}\sigma} exp(-\frac {(y_i - \beta x_i)^2}{2\sigma^2})

2. 贝叶斯学派

贝叶斯学派认为参数本身存在一个概率分布，并没有唯一真实参数，参数空间里的每个值都可能是真实模型使用的参数，区别只是概率不同，所以就引入了先验分布（prior distribution）和后验分布（posterior distribution）来找出参数空间每个参数值的概率

根据选择后验分布的某个未知特征量，贝叶斯估计可以分3种方式：

1. 选择后验分布的最大值作为估计，成为\beta的最大后验估计
2. 选择中位数作为估计值，称为\beta的后验中位数估计
3. 选择后验分布的期望值作为估计，成为\beta的后验期望估计。这种方式最为复杂，但也最准确，通常也简称贝叶斯估计

2.1. 最大后验估计

最大后验估计，maximum a posteriori estimation，简称 MAP

最大似然估计其实有一个很致命的问题，就是过拟合。因为最大似然的目的是让样本数据出现的概率最大化，以此来求得最接近真实参数的估计值。如果数据样本太小，比如抛硬币，刚好十次都是正面，难道你能说抛硬币正面的概率是100%？

那如果我们在似然的基础之上，增加一个先验概率会怎么样？

\hat \theta_{MAP} (x) \\ = \mathop{\arg\max}_{\theta} p(x|\beta) * p(\beta) \\ = \mathop{\arg\max}_{\theta} \prod_{i=1}^{n} p(x_i|\beta) * p(\beta)

这就是 MAP 的定义

要让后验概率最大，取对数，求极值

\hat \theta_{MAP} (x) \\ = \mathop{\arg\max}_{\theta} \prod_{i=1}^{n} p(x_i|\beta) * p(\beta) \\ = \mathop{\arg\max}_{\theta} \sum_{i=1}^{n} ln(p(x_i|\beta)) + ln(p(\beta))

似然前面我们已经知道了，先验怎么求呢？

假设我们上面的数据，是人体身高和体重的关系，通常认为 体重 = 身高 × 0.7，所以\beta_0 = 0.7的可能性最大

此外，和最大似然估计中的\xi类似，对于任意一组样本数据(x_i,y_i)，参数\beta肯定服从正态分布。因此我们采用均值为0.7，方差为0.1的正态分布来描述我们的先验\beta

注意：这个先验不一定是要很准确的，可以目测估计即可。因为样本数据越多，先验的作用就会越小

p(\beta) = \frac {1}{\sqrt{2\pi}\sigma} e^{-\frac {(\beta - \mu)^2}{2\sigma^2}}

从最大后验开始，就有点贝叶斯的意思了

2.2. 贝叶斯估计：后验期望估计

太复杂了，先放本书，压压惊。茆诗松的贝叶斯统计，写的是真好

https://bbs.pinggu.org/thread-6442067-1-1.html

贝叶斯估计是 MAP 的进一步增强，MAP 只是考虑了后验分布里的一个最大值，但是贝叶斯估计需要考虑整个后验分布，并取它的期望。所以，这里就不得不考虑p(x)了

贝叶斯后验定义：

p(\beta|x) = \frac {p(x|\beta) p(\beta)}{p(x)}

根据全概率公式：p(B) = \sum {i=1}{n} p(A_i)p(B|A_i)

我们可以得到分布的表达式为：p(x) = \int_{\beta} p(x|\beta)p(\beta)d\beta

当\beta已知的情况下，p(x|\beta) 就是极大似然估计的联合密度函数，即：

p(x|\beta) = \prod_{i=1}^{n} p(x_i|\beta)

最终得到：

p(\beta|x) = \frac {(\prod_{i=1}^{n} p(x_i|\beta)) p(\beta)}{\int_{\beta} (\prod_{i=1}^{n} p(x_i|\beta)) p(\beta)d{\beta}}

但是这个后验计算起来非常复杂，因为我们要把所有的后验找出来。所以这里面有一个优化就共扼先验