很多时候我们有一堆数据，并且也知道数据的基本模型，但是不知道模型的参数是什么。这是基本的机器学习过程，这个过程就叫参数估计

比如我们现在就有一堆数据，模型是y = \beta_0 x + \beta_1 + \xi = \beta^T X + \xi，我们要求\beta

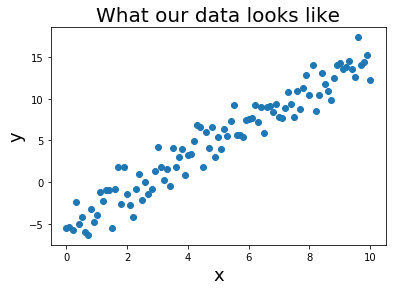
常见的计算\beta的手段有：

1. 最小二乘法
2. 最大似然估计
3. 最大后验估计
4. 贝叶斯估计

但是这几种估算方法的背后，其实代表了两类学术派别，也就是大家学习贝叶斯的时候经常听到的，频率学派和贝叶斯学派

今天来捋捋这两种学派的区别和联系

线性回归产生的预测值y=\theta^T x是实值，而逻辑回归通常是要解决分类问题。用线性回归来解决分类问题效果是很差的

分类问题在生活中是很常见的，二项逻辑回归模型有如下的条件概率分布

1. 成功概率：P(Y=1|X) = \frac {1}{1+e^{-\theta^T x}}
2. 失败概率：P(Y=0|X) = 1- \frac {1}{1+e^{-\theta^T x}}