神说,要有正态分布,就有了正态分布。
神看正态分布是好的,就让随机误差服从了正态分布。
— 创世纪—数理统计
转载自:https://cosx.org/2013/01/story-of-normal-distribution-1
1. 正态分布,熟悉的陌生人
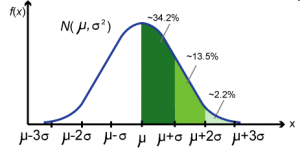
学过基础统计学的同学大都对正态分布非常熟悉。这个钟形的分布曲线不但形状优雅,它对应的密度函数写成数学表达式
\displaystyle f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{{(x-\mu})^2}{2\sigma^2}}也非常具有数学的美感。其标准化后的概率密度函数
\displaystyle f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}更加的简洁漂亮,两个最重要的数学常量 (\pi)、(e) 都出现在这公式之中。在我个人的审美之中,它也属于 top-N 的最美丽的数学公式之一,如果有人问我数理统计领域哪个公式最能让人感觉到上帝的存在,那我一定投正态分布的票。因为这个分布戴着神秘的面纱,在自然界中无处不在,让你在纷繁芜杂的数据背后看到隐隐的秩序。